O exercício 6.12 apresenta coeficientes de arraste para o aerofólio 00 12 da NASA. Você calculou a média, variância e o desvio padrão da mostra de todos aqueles coeficiente.
- Encontre a medida e os partes superior inferior dos coeficientes de arraste.
- Construa um diagrama de caixa de dados.
- Isole a maior observação e refaça os itens a e B. Comente sua resposta.
Passo 1
Letra a:
Ordene os valores dos dados do menor para o maior:
74, 79, 80, 81, 82, 83, 84, 85, 100
Como o número de pontuações é ímpar, a mediana é o valor médio do conjunto de dados classificado:
O primeiro quartil é a mediana dos valores dos dados abaixo da mediana (ou em 25% dos dados):
O terceiro quartil é a mediana dos valores de dados acima da mediana (ou em 75% dos dados):
Passo 2
Letra b:
Os bigodes do boxplot estão no valor mínimo e máximo. A caixa começa no quartil inferior, termina no quartil superior e tem uma linha na mediana.
O quartil inferior está em 25% da lista de dados classificados, a mediana em 50% e o quartil superior em 75%.
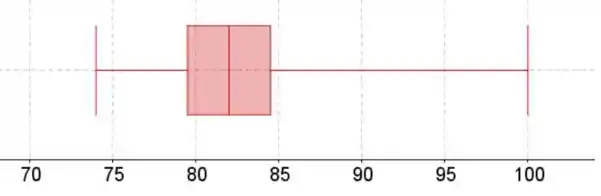
Passo 3
Letra c:
Ignore o valor de dados 100.
Ordene os valores de dados do menor para o maior:
74, 79, 80, 81, 82, 83, 84, 85, 100
Como o número de pontuações é par, a mediana é a média dos dois valores médios do conjunto de dados classificado:
O primeiro quartil é a mediana dos valores dos dados abaixo da mediana (ou em 25% dos dados):
O terceiro quartil é a mediana dos valores de dados acima da mediana (ou em 75% dos dados):
Passo 4
Os bigodes do boxplot estão no valor mínimo e máximo. A caixa começa no quartil inferior, termina no quartil superior e tem uma linha na mediana.
O quartil inferior está em 25% da lista de dados classificados, a mediana em 50% e o quartil superior em 75%.
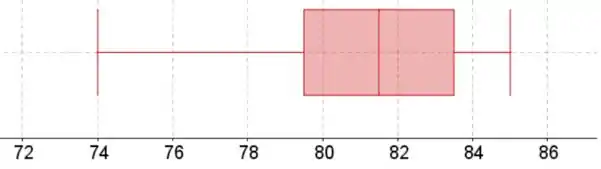
A distribuição com o valor 100 parece ser distorcida à esquerda, enquanto a distribuição sem o valor 100 parece estar inclinado para a direita.
O centro de ambos os conjuntos de dados é praticamente o mesmo, porque as medianas diferem apenas em 0.49.
O spread para os dados com o valor 100 é maior do que o spread para os dados sem o valor 100, porque a largura entre os bigodes é maior para os dados com outlier.
Resposta
- Mediana: 82
- Veja o boxplot
- Mediana: 81.51
Quartis: 79.5, 84.5
Quartis: 79.5, 84.5