Reconsidere os dados do consumo de energia do exercício 6.21. Construa um diagrama de caixa dos dados escreva uma interpretação do gráfico. Como o diagrama de caixas comparem valor interpretativo, ao diagrama original de ramo e folhas?

Ordene os valores dos dados do menor para o maior:

1.04. 2,3, 2,91, 3,3. 6,8, 6,88, 16,2. 17,43, 30,89, 36,92, 37,03, 38,43, 44,48, 71,54, 73,63, 101,8, 107,34, 154,34, 200,66, 303,33, 519,04, 946,27, 1671,23

Como o número de pontuações é ímpar, a mediana é o valor médio do conjunto de dados classificado:

O primeiro quartil é a mediana dos valores dos dados abaixo da mediana (ou em 25% dos dados):

O terceiro quartil é a mediana dos valores de dados acima da mediana (ou em 75% dos dados):

Os bigodes do boxplot estão no valor mínimo e máximo. A caixa começa no quartil inferior, termina no quartil superior e tem uma linha na mediana.

O quartil inferior está em 25% da lista de dados classificados, a mediana em 50% e o quartil superior em 75%.

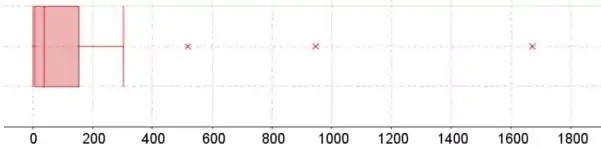
O boxplot oferece um valor interpretativo tão bom quanto o diagrama ramo e folha, porque observamos os mesmos outliers no boxplot e na distribuição parece estar fortemente inclinado para a direita em ambas as telas gráficas.

O diagrama de ramo e folha também nos permite determinar os valores dos dados do conjunto de dados e os percentis da distribuição, o que não é possível com o boxplot.