Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 7.Exercícios - Ex. 39
O Exercício 72 do Capitulo 1 forneceu as seguintes observações sobre a medida de absorção do receptor (volume de distribuição ajustado) de uma amostra de 13 pessoas saudáveis: , .
a. É plausível que a distribuição da população da qual essa amostra foi selecionada seja normal?
b. Calcule o intervalo para o qual possamos ter de confiança de que pelo menos de todas as pessoas saudáveis da população tenham ajustado os volumes da distribuição ajustados incluídos entre os limites do intervalo.
c. Preveja o volume da distribuição ajustado de uma única pessoa saudável, calculando o intervalo de previsão de 95%. Como a amplitude desse intervalo se compara com o intervalo calculado na parte (b)?
Passo 1
a. plot da probabilidade normal
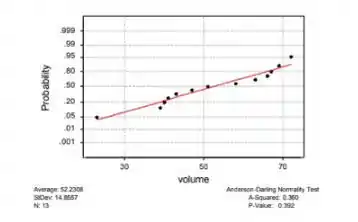
Com base no gráfico acima, gerado pelo Minitab, é plausível que a distribuição da população seja normal.
Passo 2
b. Exigimos um intervalo de tolerância. (da tabela A6, com 95% de confiança, k=95, en=13, tev=3,081.
Passo 3
c. o intervalo de predição, com
Resposta
Distribuição da população é normal
b.
c.