O Exercício 14 apresentou dados sobre o peso corporal x e a taxa de depuração metabólica/peso corporal y. Considere as seguintes funções intrinsecamente lineares para especificar a relação entre as duas variáveis: (a) ln(y) versus x, (b) ln(y) versus ln(x), (c) y versus ln(x), (d) y versus 1/x e (e) ln(y) versus 1/x. Use qualquer gráfico de diagnóstico e análise apropriados para determinar qual dessas funções você selecionaria para especificar um modelo probabilístico. Explique seu raciocínio.
Passo 1
Na solução, não haverá cálculos mostrados, apenas gráficos e a análise.
O gráfico de dispersão a seguir sugere que, usando esses dados, um modelo linear não é apropriado e não é uma boa escolha. As tabelas a seguir consistem em dados, resíduos e tudo o que é necessário para o gráfico de dispersão e o gráfico de resíduos de x versus y. A primeira tabela são os dados necessários para o gráfico de dispersão, a segunda tabela é para o gráfico de resíduos. Os resíduos são muito grandes; assim, os dados não suportam o modelo linear



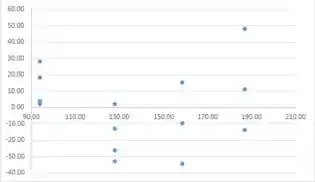
Passo 2
O gráfico de dispersão e o gráfico de resíduos a seguir sugerem que, usando esses dados, um modelo linear pode ser apropriado. As tabelas a seguir consistem em dados, resíduos e tudo o que é necessário para o gráfico de dispersão e o gráfico de resíduos de x versus . A primeira tabela são os dados necessários para o gráfico de dispersão, a segunda tabela é para o gráfico de resíduos.
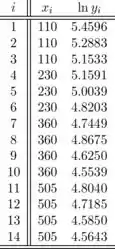
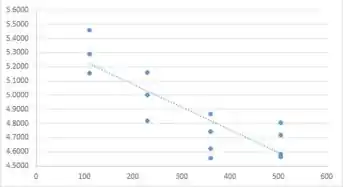


O gráfico de dispersão e o gráfico de resíduos a seguir sugerem que, usando esses dados, um modelo linear pode ser apropriado. As tabelas a seguir consistem em dados, resíduos e tudo o que é necessário para o gráfico de dispersão e o gráfico de resíduos de versus . A primeira tabela são os dados necessários para o gráfico de dispersão, a segunda tabela é para o gráfico de resíduos.
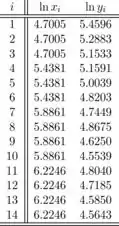
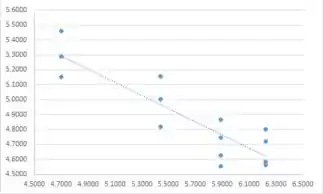
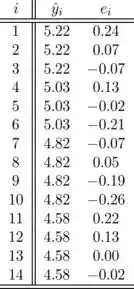

O gráfico de dispersão e o gráfico de resíduos a seguir sugerem que, usando esses dados, um modelo linear não é apropriado e não é uma boa escolha. As tabelas a seguir consistem em dados, resíduos e tudo o que é necessário para o gráfico de dispersão e o gráfico de resíduos de versus y. A primeira tabela são os dados necessários para o gráfico de dispersão, a segunda tabela é para o gráfico de resíduos. Os resíduos são bastante grandes; assim, o modelo linear não é apropriado.

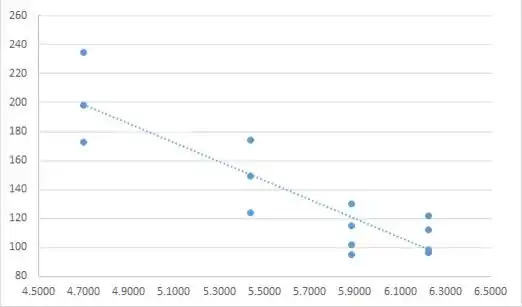

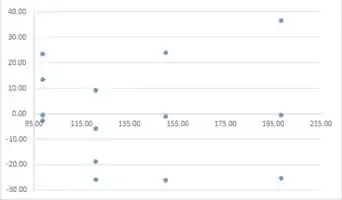
O gráfico de dispersão e o gráfico de resíduos a seguir sugerem que, usando esses dados, um modelo linear não é apropriado e não é uma boa escolha. As tabelas a seguir consistem em dados, resíduos e tudo o que é necessário para o gráfico de dispersão e o gráfico de resíduos de 1/x versus y. A primeira tabela são os dados necessários para o gráfico de dispersão, a segunda tabela é para o gráfico de resíduos. Os resíduos são bastante grandes; assim, o modelo linear não é apropriado. Os resíduos são grandes; o modelo linear não é apropriado
Passo 3
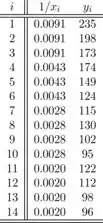
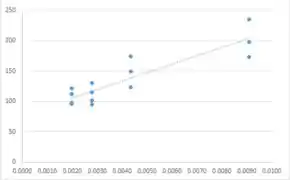


O gráfico de dispersão e o gráfico de resíduos a seguir sugerem que, usando esses dados, um modelo linear não é apropriado e não é uma boa escolha. As tabelas a seguir consistem em dados, resíduos e tudo o que é necessário para o gráfico de dispersão e o gráfico de resíduos de 1/x versus . A primeira tabela são os dados necessários para o gráfico de dispersão, a segunda tabela é para o gráfico de resíduos. Os resíduos são bastante grandes; assim, o modelo linear não é apropriado. Os resíduos são grandes; modelo linear não é apropriado.
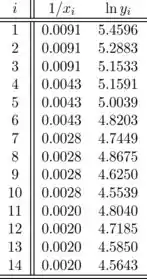
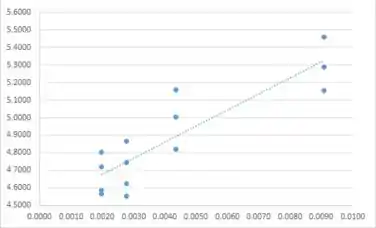

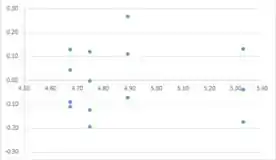
Duas transformações podem ser apropriadas. Deve-se investigar mais para ver qual desses dois é melhor. Essas duas transformações são
O coeficiente de correlação e o coeficiente de determinação para os dados transformados e dados em (a) são
e para os dados transformados e dados em (b) são
ambos, coeficiente de correlação e coeficiente de determinação, são maiores para a transformação em (b), também, os resíduos são um pouco menores para a transformação em (b); assim, a transformação em (b), que também remove a curvatura e para a qual o gráfico de resíduos é aleatório (isso é bom), é a melhor. Isso indica que o modelo de poder é o melhor ajuste para os dados originais
Isso se mantém porque, usando a transformação apropriada dada em (b), o modelo linear é o melhor ajuste.
Resposta
Ver o desenvolvimento