Enunciado
Probabilidade e Estatística - Walpole - Probabilidade e Estatística para Engenharia e Ciências- Ed: 8º - Capítulo 10.Exercícios - Ex. 74
No Exercício 10.41, teste a hipótese, no nível de significância 0,05, de que contra a alternativa e são as variâncias para o número de organismos por metro quadrado nas duas localizações diferentes do rio Cedar Run.
Passo 1
Falaaaa moçadinha, show de bola?
Como diz o Homem de ferro “Eu tenho um plano. Ataque!”
Bora atacar esse problemaaaaaaa junto comigoo.
Os dados a seguir fornecem as medidas de densidade, em número de organismos por metro quadrado, nas duas estações de coleta.
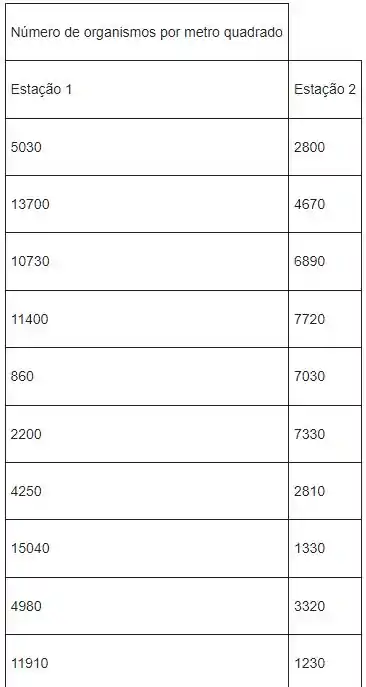
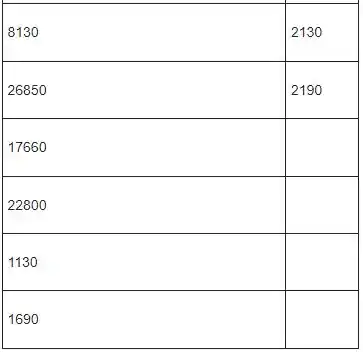
Passo 2
Reivindicação: Podemos aplicar o teste F para testar variações. Agora organizamos o procedimento de teste e os cálculos são fornecidos abaixo.
Procedimento:
A hipótese nula e alternativa é
Nivel de significância,
Regra de decisão: Rejeitar
A estatística de teste computada é então dada por,
Onde estão as variações calculadas a partir das duas amostras. Se as duas populações forem aproximadamente normalmente distribuídas e a hipótese nula for verdadeira, a razão é um valor da distribuição F com graus de liberdade.
Passo 3
Estatísticas resumidas
Estação 1:
Estação 2:
Calculando a estatística de teste
Graus de liberdade
Assim, o valor da estatística de teste é
Passo 4
Agora, iremos determinar o valor de P para o teste F
O valor P do teste é 0,0005, que é menor que 0,05. Assim, rejeite a hipótese nula
a um nível de significância de 5%.
Há fortes evidências para apoiar a alegação de que as variações para os dois locais são significativamente diferentes.
“Às vezes é preciso aprender a correr antes de começar a andar”
Resposta
Resposta nos passos.