Nos exercícios 17 a 34, encontre a média, a mediana e a moda dos dados, se possível. Se quaisquer dessas medidas não puderem ser encontradas ou não representarem o centro dos dados, explique o porquê.

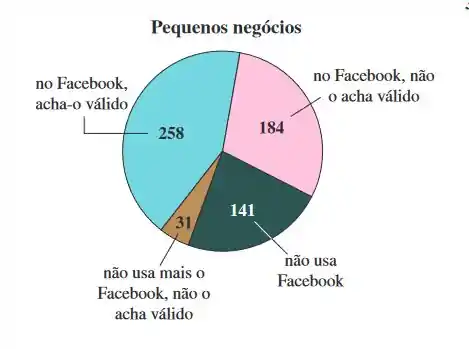
Facebook - O gráfico de pizza a seguir mostra as respostas de uma amostra de 614 proprietários de pequenos negócios que foram indagados sobre sua presença no Facebook. (Adaptado de: Manta.)

Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!

Variáveis qualitativas ​​colocam os indivíduos em uma categoria, enquanto uma variável quantitativa é uma variável numérica.

A média não pode ser encontrada, porque a variável é uma variável qualitativa (os valores são: quantidade do primeiro salário, tentativa de encontrar um emprego, número de decisão, dinheiro necessário, pagando contas, tentando economizar, como é difícil se separar dos pais) e a média só pode ser encontrada para uma variável quantitativa (com valores de dados numéricos).

A mediana não pode ser encontrada, porque a variável é uma variável qualitativa (dados

valores são quantidade do primeiro salário, tentativa de encontrar um emprego, número de decisão, dinheiro necessário, pagando contas, tentando economizar, como é difícil se separar dos pais) e a mediana só pode ser encontrada para uma variável quantitativa (com dados numéricos valores).

A moda é o valor de dados que ocorre com mais frequência no conjunto de dados. Dentro do estojo de uma variável qualitativa, a moda é a categoria com maior frequência, que é "no Facebook, acha-o válido" neste caso.