Enunciado
Probabilidade e Estatística - Estatística Aplicada Farber e Larson- Ed: 6º - Capítulo 2.3 - Ex. 52
Encontrando a média de uma distribuição de frequência - Nos exercícios 49 a 52, aproxime a média da distribuição de frequência.
52. Idades - As idades dos moradores de Medicine Lake, Montana, em 2010. (Fonte: U.S. Census Bureau.)
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
Primeiramente, vamos fazer uma tabela
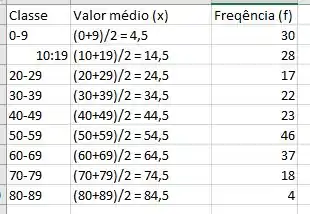
Agora, vamos determinar a soma de todas as frequências
A média da distribuição de frequência é a soma dos produtos dos pontos médios e as frequências correspondentes, dividida pela soma das frequências
Substituindo os valores, nós temos que
Com isso, nós temos que
O que nos dá aproximadamente
Resposta
Exercícios de Livros Relacionados
Se 0α1 , uma média aparada a 100 α % é obtida eliminando 100 α % das menores observações e 100 α % das maiores observações e calculando-se a média aritmética das restantes. Por exemplo, se tivermos 10
Suponha que X tem um Distribuição discreta uniformeUma amostra aleatória de N = a 36 e selecionada dessa população. Encontre a probabilidade da média amostral ser maior do que 2,1, porém menor do que
Suponha que Θ 1 e Θ 2 sejam estimadores não tendenciosos do parâmetro. Sabemos que . Qual é o melhor estimador e em que sentido é melhor? Calcule a eficiência relativa dos dois estimadores.
Mostre queé um estimador tendencioso de sigma ^2. Encontre a quantidade de tendenciosidade no estimador. O que acontece a tendência à medida que o tamanho da amostra aumenta?
Dados sobre a força (libra-força) de remoção de conectores usados em um motor de automóveis são os seguintes . Calcule a estimativa pontual da força média de remoção de todos os conectores da populaçã