Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 12.Problemas - Ex. 34
A prefeitura de uma cidade quer estimar a proporção p dos moradores favoráveis à
mudança do horário comercial, com o intuito de economizar combustível. Essa propor-
ção deverá ser estimada com um erro máximo de 5%, a um nível de 90% de confiança.
(a) Que tamanho deverá ter a amostra se a proporção p esperada deve estar entre 20%
e 50%? (Justifique a resposta.)
(b) Numa amostra de 400 moradores, 160 foram favoráveis à mudança; qual seria o
intervalo de confiança para p, nesse caso,?
Passo 1
- Considerando que a população seja normalmente distribuída:
- Do enunciado, podemos encontrar:
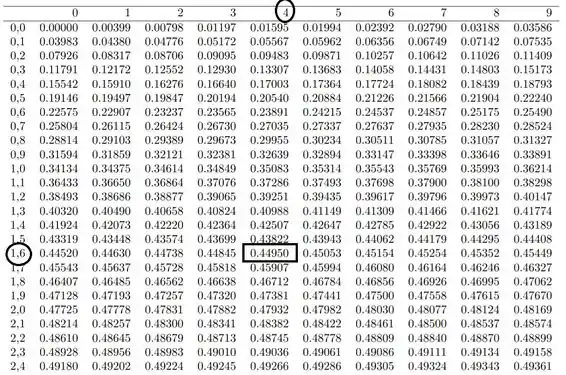
Passo 2
Construindo nosso intervalo de confiança:
Resposta
- N=269 amostras.
Exercícios de Livros Relacionados
Uma pessoa gaba-se de adivinhar qual será o resultado do lance de uma moeda, mas épreciso que os presentes não o perturbem com pensamentos duvidosos. Para testar talcapacidade, lançou-se uma moeda per
Um fabricante garante que 90% dos equipamentos que fornece a uma fábrica estão deacordo com as especificações exigidas. O exame de uma amostra de 200 peças desse equi-pamento revelou 25 defeituosas. T
Para o problema anterior, construa IC( σ 2 ; 90%) e descreva as suposições consideradaspara obtenção da resposta.
Numa pesquisa realizada com 2.000 proprietários de carros na cidade de São Paulo, 800responderam que pretendem mudar de carro no decorrer do próximo ano. Dê um IC de90% para a proporção de todos os pr