Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 5.2 - Ex. 4c

A função de probabilidade conjunta entre as variáveis aleatórias X e Y é apresentada na próxima tabela.

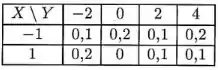
  1. Obtenha as tabelas marginais de frequência.
  2. X e Y são independentes?
  3. Calcule a covariância e a correlação entre X e Y.

Passo 1

  1. Para obter a Covariância temos que calcular o valor esperado de X e de Y e de XY, vamos começar com E X   e   E ( Y ) que são mais simples:

E X = - 1 × 0,6 + 1 × 0,4 = - 0,2

E Y = - 2 × 0,3 + 0 × 0,2 + 2 × 0,2 + 4 × 0,3 = 1

Passo 2

Para calcular E X Y , como essas variáveis não são independentes, precisamos pegar todos os pares x , y (que podemos observar na tabela conjunta), e para cada par multiplicar o produto deles pela probabilidade desse par ocorrer (que se encontra na tabela conjunta), e em seguida somar o resultado para todos os pares:

E X Y = - 2 × - 1 × 0,1 + - 2 × 1 × 0,2 + 0 × - 1 × 0,2 + … + [ 4 × 0,1 × 0,1 ]

E X Y = - 0,6

Passo 3

Logo a C o v X , Y = E X Y - E X E ( Y )

C o v X , Y = - 0,6 - - 0,2 × 1 = - 0,4

Passo 4

Antes de calcular a correlação temos que calcular V a r X   e   V a r Y :

V a r X = ∑ i X i - X - × P ( X i )

Onde a média da variável (no caso X - ) é E X :

V a r X = - 1 - - 0,2 2 × 0,6 + 1 - - 0,2 2 × 0,4 = 0,96

Da mesma forma:

V a r Y = ∑ i Y i - Y - × P ( Y i ) = 5,8

Passo 5

Podemos calcular a correlação, através da fórmula:

ρ X , Y = C o v X , Y V a r X V a r Y

E podemos lembrar que a correlação é um valor que deve sempre estar entre -1 e 1:

ρ X , Y = - 0,17

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em dias chuvosos, Joe chega atrasado ao trabalho com probabilidade 0,3; em dias não chuvosos, ele chega atrasado com probabilidade 0,1 . Com probabilidade 0,7, choverá amanhã.(a) Determine a probabili
Considere uma amostra de 3 bolas retirada da seguinte maneira: começamos com uma urna contendo 5 bolas brancas e 7 bolas vermelhas. Em cada rodada, uma bola é retirada da urna e sua é cor anotada. A b
Há 3 moedas em uma caixa. Uma delas tem duas caras, outra é honesta e a terceira é uma moeda viciada que dá cara em 75% das vezes. Quando uma das 3 moedas é selecionada aleatoriamente e jogada, ela dá
Há 15 bolas de tênis em uma caixa, das quais 9 nunca foram usadas anteriormente. Três das bolas são escolhidas aleatoriamente, utilizadas em uma partida, e então devolvidas para a caixa. Mais tarde, o
Um baralho de 52 cartas é embaralhado e então dividido em dois maços de 26 cartas cada. Uma carta é retirada de um dos maços; ela é um ás. O ás é então colocado no segundo maço. Este maço é então emba