Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 13.Exercícios - Ex. 14
Se houver pelo menos um valor x no qual foi feita mais de uma observação, existe um procedimento de teste formal para testar
Suponha que se façam observações em x1, x2, ..., xc. Sejam Y11, Y12, ..., Y1n1 as n1 observações quando x x1; ...; Yc1, Yc2, ..., Ycnc as nc observações quando x xc. Com n ni (número total de observações), SQE tem n 2 gl. Dividimos SQE em duas partes, SQEP (erro puro) e SQFA (falta de aderência), como a seguir:
As ni observações em xi contribuem com ni 1 gl para SQEP, de modo que o número de graus de liberdade de SQEP é i (ni 1) n c e o de SQFA é n 2 (n c) c 2. Seja QMEP SQEP/(n c) e QMFA SQFA/(c 2). Logo, é possível mostrar que, embora E(QMEP) 2 , independentemente de H0 ser ou não verdadeira, E(QMFA) 2 se H0 for verdadeira e E(QMFA) 2 se H0 for falsa
Os dados a seguir foram apresentados no artigo “Changes in Growth Hormone Status Related to Body Weight of Growing Cattle” (Growth, 1977, p. 241-247), com x peso corporal e y taxa de depuração metabólica/peso corporal
a. Teste H0 versus Ha ao nível 0,05 usando o teste de falta de aderência que acabamos de descrever. b. Um gráfico de dispersão dos dados sugere que a relação entre x e y é linear? Como isso se compara com o resultado da parte (a)? (Foi usada no artigo uma função de regressão não-linear.)
Passo 1
Para aceitar ou rejeitar hipóteses nulas, usaremos a próxima estatística:
E rejeitamos a hipótese nula se .
Nesta tarefa temos c=4 observações de e para cada o número de as observações são , respectivamente. Precisamos dar respostas nas próximas perguntas
- Agora iremos testar a hipótese . Nós temos o seguinte:
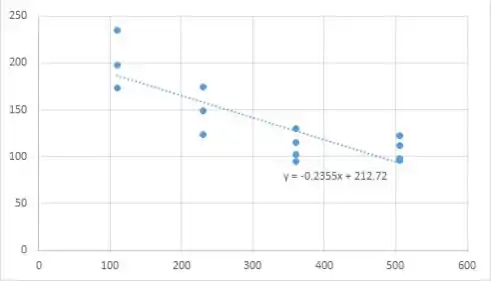
- Agora vamos representar o gráfico de dispersão para dados x e y. Como podemos ver no gráfico abaixo em cada grupo apenas uma observação está próxima da linha de ajuste e as demais observações estão distantes desta linha. Eles não são bem correlacionados. Mas a partir do teste acima aprovamos que o modelo de regressão para tais dados é linha de regressão linear
Agora precisamos calcular o SSPE e SSLF. Temos o seguinte:
Primeiro precisamos encontrar o coeficiente e . Para calcular esses coeficientes e SSE, usaremos as próximas fórmulas
A partir dos dados fornecidos temos o seguinte:
Passo 2
Agora as estatísticas necessárias para calcular a estatística F são calculadas e apresentadas abaixo:
Como nossa estatística F é menor que o valor crítico aceitaremos hipóteses nulas. Então, nossa linha de regressão é linear
Resposta
Ver o desenvolvimento.