Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 13.Exercícios - Ex. 13

Lembre-se de que ˆ 0 ˆ 1x tem uma distribuição normal, com valor esperado 0 1x e variância de modo que tem uma distribuição normal padronizada. Se S SQE/(n2) for substituída por , a variável resultante terá uma distribuição t com n 2 gl. Por analogia, qual é a distribuição de qualquer resíduo padronizado? Se n 25, qual é a probabilidade de um determinado resíduo padronizado ficar fora do intervalo (2,50; 2,50)?

Passo 1

Seja x * ser um valor fixo de x. Para a variável aleatória

Y ^ = β ^ 0 + β ^ 1 x *

vale o seguinte:

A média da variável aleatória   Y ^ é

E Y ^ = E β ^ 0 + β ^ 1 x *   =   β 0 + β 1 x *

o que significa que   Y ^ é um estimador imparcial para   β 0 + β 1 x * .

A variância da variável aleatória   Y ^ é

O desvio padrão é a raiz quadrada da expressão. Ao substituir (estimar) σ por s você obtém a estimativa da variância e/ou desvio padrão da variável aleatória   Y ^ .

Variável aleatória   Y ^ tem distribuição normal.

Os residuais dados por

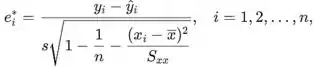
são os resíduos padronizados.

O desvio padrão do resíduo   Y i - Y ^ i é

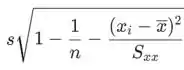
Passo 2

A distribuição de resíduos padronizados é uma distribuição t com n-2 graus de liberdade, em analogia com as informações fornecidas no exercício.

Quando n=25, E i * (variável aleatória) tem distribuição t com 25-2=23 graus de liberdade. A probabilidade de que o resíduo caia fora do intervalo

- 2.50 ,   2.50

É

P E i * ≤   - 2.50 + P E i * ≥ 2.50 = 2 P E i * ≥ 2.50 = 2 ∙ 0.01 = 0.02

Uma tabela no apêndice foi usada para calcular os valores de t.

Resposta

Uma distribuição t com n-2 graus de liberdade; a probabilidade é 0.02

Exercícios de Livros Relacionados

11-96. Minimos Quadrados Ponderados. Suponha que estejamosajustando a linha a variância porém. de Y depen-de do nível de x; ou seja. V Y i ∣ x i = σ i 2 = σ 2 w i i = 1,2 , … , n sendo as constantes w
11-98. Suponha que estejamos interessados em ajustar um modelode regressão linear simples em que a interseção, n,seja conhecida.a) Encontre o estimador de mínimos quadrados para b) Qual é a variância
11-93. Considere o modelo de regressão linear simples estando os erros e não correlacionados.a) Mostre que E σ ^ 2 = E M Q 2 = σ 2 b)Mostre que E M Q R = σ 2 + β i 2 S α
Refira-se aos dados do exercício 11-4 sobreo preço de venta de casas y e taxas pagas x.a)Encontre os resíduos para o modelo de mínimos quadrados.b)Prepare um gráfico de probabilidade normal dos resídu
Refira-se ao exercício 11-10 que apresenta dados sobre concentração de cloreto y e área da rodovia x.a)Que proporção da variabilidade total do aumento da pressão sanguínea é explicada pela pressão son