Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 4.4 - Ex. 23

Numa indústria pretende comprar 3 lotes de peças que são produzidas por dois fornecedores, A e B . Ela inicia, comprando de um dos fornecedores escolhido ao acaso, se ficar satisfeita com o material entregue, compra o próximo lote do mesmo fornecedor. Se não ficar satisfeita, troca o fornecedor. Admita que para cacla lote o índice de satisfação é de 80 % e de 70 % para A e B , respectivamente. Calcule a média e a variância do número de lotes fornecidos por A .

Passo 1

Eai,tudo bem? Bora resolver mais um exercício?

O exercício nos pede para calcularmos a média e variância do número de lotes fornecidos por A . Mas antes, para facilitar nossos cálculos, vamos construir uma árvore de porobabilidades, ok?.

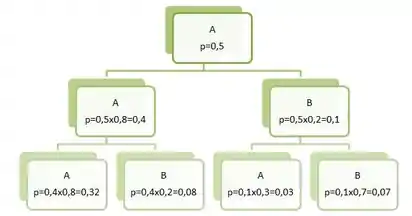
Passo 2

Seja X : número de lotes fornecidos por A . Assim, temos:

x = 0 ⇒ P x = 0 = 0,245

x = 1 ⇒ P x = 1 = 0,07 + 0,105 + 0,03 = 0,205

x = 2 ⇒ P x = 2 = 0,08 + 0,03 + 0,12 = 0,23

x = 3 ⇒ P x = 3 = 0,32 .

Construindo então a função de probabilidade, temos que:

Passo 3

Assim, calculando a esperança temos que:

E X = ∑ x × p i = 0 × 0,245 + 1 × 0,205 + 2 × 0,230 + 3 × 0,320 = 1,625 .

Ou seja, a média é 1,625 de lotes fornecidos por A .

E também,

E X 2 = ∑ x 2 × p i = 0 2 × 0,245 + 1 2 × 0,205 + 2 2 × 0,230 + 3 2 × 0,320 = 4,005 .

Logo,

V a r X = E X 2 - E X 2 = 4,005 - 1,625 2 = 1,364 .

Resposta

Logo, a média é 1,625 e a variância 1,364 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Obtenha a média e a variância da v.a. X dos Problemas 1 e 2.
Sendo X uma variável aleatória com função de probabilidade dada a seguir, obtenha as medidas de posição μ ,M deM o .
Um atacadista recebe de vários fornecedores uma certa peça para recenda. A peça é produzida com material de qualidade diferente e, portanto, tem o custo diferenciado. Levando em conta a proporção forn
Você está indeciso em comprar uma televisão e decide avaliar algumas informações estatísticas, fornecidas pelo fabricante, sobre a duração (em horas) do tubo de imagem.Com que marca você ficaria? Just
A pulsação de 10 estudantes no início de uma prova de estatística foram as seguintes (em batimentos por minuto): 80, 91, 84, 86, 93, 88, 80, 89, 85 e 86. Calcule a média e a variância desse conjunto d