Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 4.2 - Ex. 4
Sendo X uma variável aleatória com função de probabilidade dada a seguir, obtenha as medidas de posição
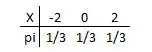
Passo 1
A média de uma variável aleatória será dada por:
Passo 2
A moda é o valor com maior probabilidade de ocorrer, como todos tem a mesma probabilidade de ocorrer, vamos ter uma situação amodal, ou seja, sem moda.
Passo 3
Em mediana, como não temos a seguinte situação:
vamos utilizar o valor médio do intervalo, no caso, a mediana será dada por .
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Determine a médica e avariada da variável aleatória do Exercício 3-16.
Determine a médica e avariada da variável aleatória do Exercício 3-19.
A faixa da variável aleatória X é (0,1,2,3,x), em que x é uma incógnita. Se cada valor for igualmente provável e a média de X for igual a 6, determine x.
Determine a médica e avariada da variável aleatória do Exercício 3-20.
Determine a médica e avariada da variável aleatória do Exercício 3-18.