Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 14.Exercícios - Ex. 50
Em seu livro Empirical Model Building and Response Surfaces – Construção de Modelos Empíricos e Superfícies de Resposta. (John Wiley, 1987). G. E. Box e N. R. Draper descrevem um experimento com três fatores. Os dados mostrados na tabela a seguir representam uma variação do experimento original na página 247 do referido livro. Suponha que esses dados tenham sido coletados em um processo de fabricação de semicondutores.
A resposta é a média de três leituras da resistividade para uma única pastilha. Ajuste um modelo quadrático para essa resposta.
A resposta é o desvio-padrão das três medidas da resistividade. Ajuste um modelo linear para essa resposta.
Onde você recomendaria que estabelecêssemos , e , se o objetivo fosse manter a resistividade média em e minimizar o desvio-padrão?
Passo 1
Bom galera, para resolvermos esse problema a gente considera o modelo para observações e na notação matricial. Para obtermos o modelo de regressão que funcione precisamos usar a formula:
O vetor dos resíduos é dado por: .
O estimador da variante é .
A regressão da soma dos quadrados é:
O coeficiente de determinação múltipla é .
Então nós chegamos no modelo:
Passo 2
Beleza, agora usando o Minitab para encontrar a equação de regressão. Nós encontraremos:
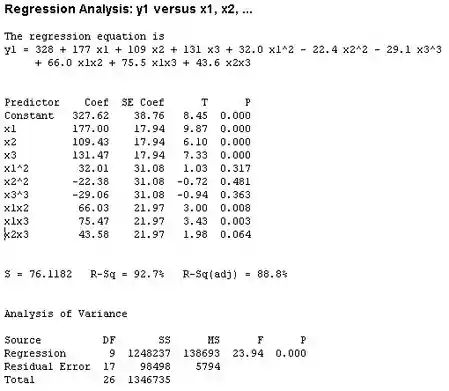
Com os resultados temos os valores dos t-testes para os coeficientes de significância de regressão , , e são maiores que . Com esses termos do modelo vamos realizar um teste .
Passo 3
Show de bola, fazendo a nova regressão, temos como resultados:
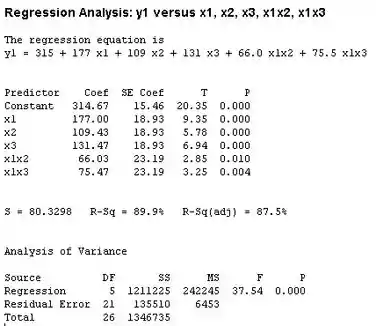
Para encontrarmos a soma extra dos quadrados para testar a significância das variáveis , , e :
Passo 4
O número de coeficiente no nosso teste de significância é . No resultado do nosso modelo completo nós encontramos . Calculando o valor do teste estatístico:
Agora, pegar o P-valor. Notamos que . Sendo , assim . Então o P-valor é maior, isso não é evidencia para concluir que as variáveis , , e são significantes, então essas variáveis podem ser retiradas do nosso modelo.
Notando que todos os coeficientes no modelo de regressão reduzida são significantes, nós obtemos o modelo de segunda ordem assim:
Passo 5
Belezinha, agora usando o modelo:
Usando o Minitab para encontrar a equação de regressão, nós temos:
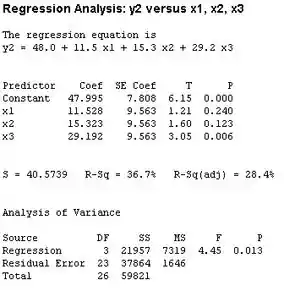
Com esse resultado nós temos os P-valores dos t-testes para a significância dos coeficientes de regressão para e , que são maiores que .
Passo 6
Então, nós usamos os termos do modelo para fazer um F-teste com as variáveis que encontramos, o teste fica:
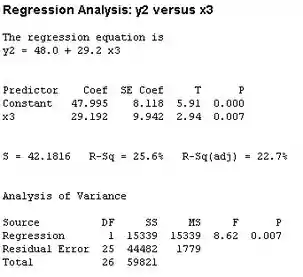
Encontrando o extra da soma dos quadrados para o teste de significância das variáveis e :
O número de coeficientes que nós testamos para a significância é . Com o resultado que nós encontramos no nosso modelo, a gente calcula o valor do teste estatístico:
Passo 7
Encontrando o P-valor. Notamos que . Temos assim que , com isso . Então, o P-valor é grande, isso não é evidencia para concluir que as variáveis e são significantes. Então, essas variáveis podem ser retiradas do nosso modelo. Ficamos com o nosso modelo assim:
Passo 8
Por fim, nós precisamos minimizar o valor de quando . Sendo dependente apenas de , e isso é dependente de uma relação linear com um coeficiente positivo, é minimizado quando é minimizado. Procuramos então na equação de quando .
Nós plotamos a superfície e fica:
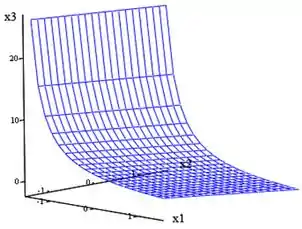
Vemos então que o valor mínimo para é obtido quando e . Encontramos o :
Resposta