Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Meyer - Aplicações a Estatística- Ed: 2º - Capítulo 2.Problemas - Ex. 21

Um lote contém n peças, das quais se sabe serem r defeituosas. Se a ordem da inspeção das peças se fizer ao acaso, qual a probabilidade de que a peça inspecionada em k -ésimo lugar ( k ≥ r ) seja a última peça defeituosa contida no lote?

Passo 1

Para que a última das r peças defeituosas seja posicionada no k -ésimo lugar, nos k - 1 lugares anteriores devem estar as demais r - 1 peças defeituosas. Além disso, para que tenhamos r - 1 peças defeituosas nos k - 1 primeiros lugares, devemos ter k - 1 - r - 1 = k - r peças sem defeitos também nesses primeiros k - 1 lugares:

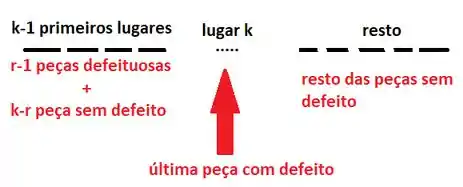
O total de formas que podemos escolher r - 1 peças defeituosas entre as r disponíveis é

C r ,   r - 1 = r

Já o total de formas que podemos escolher k - r peças sem defeito dentre as n - r disponíveis é

C n - r ,     k - r = n - r ! k - r ! n - k !

Além disso, nos k - 1 primeiros lugares podemos fazer k - 1 permutações com r - 1 e k - r repetições:

k - 1 ! r - 1 ! k - r !

Multiplicando esses três números temos o total de formas que podemos distribuir as peças da forma desejada:

r ⋅ n - r ! k - r ! n - k ! ⋅ k - 1 ! r - 1 ! k - r !

Passo 2

Para calcular a probabilidade temos que dividir o total achado no passo 1 pelo total de formas de organizar as n peças. Para isso, basta fazer uma permutação de n elementos com r e n - r repetições:

t o t a l = n ! r ! n - r !

Daí, a probabilidade é só dividir o resultado do passo 1 pelo total:

P = r ⋅ n - r ! k - r ! n - k ! ⋅ k - 1 ! r - 1 ! k - r ! n ! r ! n - r !

Ou ainda,

P = r n - r ! k - 1 ! r ! n - r ! k - r ! n - k ! r - 1 ! k - r ! n !

É um pouco feio, mas essa é a expressão...

Podemos escrever r ! = r ⋅ r - 1 ! no numerador, o que simplifica com o n - 1 ! do denominador:

P = r 2 n - r ! k - 1 ! n - r ! k - r ! n - k ! k - r ! n !

Resposta

P = r 2 n - r ! k - 1 ! n - r ! k - r ! n - k ! k - r ! n !

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sete presentes diferentes devem ser distribuídos entre 10 crianças. Quantos resultados diferentes são possíveis se nenhuma criança puder receber mais de um presente?
Quantas mãos de pôquer de cinco cartas existem?
De um grupo de 8 mulheres e 6 homens, pretende-se formar um comitê formado por 3 homens e 3 mulheres. Quantos comitês diferentes são possíveis se(a) 2 dos homens se recusarem a trabalhar juntos?(b) 2
Se 8 professores novatos tiverem que ser divididos entre 4 escolas, quantas divisões são possíveis? E se cada escola puder receber 2 professores?
Delegados de 10 países, incluindo Rússia, França, Inglaterra e os EUA, devem sentar-se lado a lado. Quantos arranjos de assentos diferentes são possíveis se os delegados franceses e ingleses tiverem q