Enunciado
Probabilidade e Estatística - Meyer - Aplicações a Estatística- Ed: 2º - Capítulo 2.Problemas - Ex. 3
a) Suponha que os três dígitos 1, 2 e 3 sejam escritos em ordem aleatória. Qual a probabilidade de que ao menos um dígito ocupe seu lugar próprio?
b) O mesmo que em (a), com os dígitos 1, 2, 3 e 4.
c) O mesmo que em (a), com os dígitos 1, 2, 3, ..., .
Passo 1
Esse é aquele tipo de problema que é melhor trabalhar com o caso complementar...
Para achar a probabilidade de que ao menos um dígito ocupe seu lugar próprio, vamos calcular primeiro a probabilidade de nenhum dígito ocupar seu lugar próprio.
No primeiro dígito temos duas opções, pode ser 2 ou 3. Todavia, não sabemos quantas opções temos para os demais dígitos pois não sabemos qual foi escolhido no primeiro...
Vamos trabalhar com dois casos:
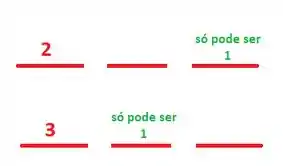
Com isso, temos duas sequências possíveis em que nenhum digito ocupa seu lugar próprio:
O total de permutações é
Logo, a probabilidade de nenhum digito ocupar seu lugar próprio é
Assim, a probabilidade de que ao menos um dígito ocupe seu lugar próprio será
Passo 2
No item (b) temos que fazer o mesmo, porém agora temos 4 dígitos. Os casos em que nenhum número ocupa seu dígito próprio são representados a seguir:
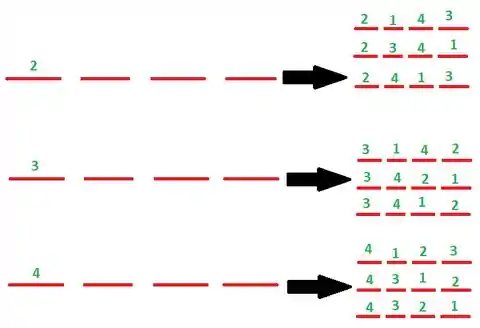
Vemos que existem 9 combinações desse tipo. O total de combinações é . Desta forma, a probabilidade de nenhum número ocupar seu lugar próprio é
Com isso, a probabilidade de ao menos um digito ocupar seu lugar próprio é
Passo 3
Para terminar o problema, vamos considerar o caso geral com dígitos. O total de combinações é , de modo que a probabilidade de ao menos um dígito ocupar seu lugar próprio é
A grande dificuldade é achar o total de casos sem nenhum dígito ocupar seu lugar próprio. No caso do item (a), tínhamos
A ideia é assim: das três opções de números, temos que escolher dois e assim fixar um dígito. Daí restam dois dígitos: escolhendo um se escolhe automaticamente o outro. Precisamos subtrair 1 pois um dos casos terá um dígito no lugar próprio.
Para o caso do item (b), começamos com , depois subtraímos e somamos 1:
A ideia é sempre ir alternando o sinal começando com até chegar no :
Portanto,
Aconselho você abrir os resultados para e para conferir certinho todos os casos e ver que a fórmula funciona!