Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 7.Exercícios - Ex. 20

  1. Mostre que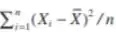é um estimador tendencioso de sigma ^2.
  2. Encontre a quantidade de tendenciosidade no estimador.
  3. O que acontece a tendência à medida que o tamanho da amostra aumenta?

Passo 1

Letra a:

Vamos mostrar que ∑ i = 1 n ( X i - X _ ) 2 / n é um estimador parcial de σ 2

E ∑ i = 1 n ( X i - X ̄ ) 2 n = 1 n E ∑ i = 1 n ( X i - X ̄ ) 2

= 1 n ∑ i = 1 n E ( X i 2 ) - n E ( X ̄ 2 )

Por que E ( X i 2 ) = μ 2 + σ 2 , e E ( X ̄ 2 ) = μ 2 + σ 2 n , então substituindo, temos:

= ( 1 - 1 n ) σ 2

Portanto ∑ i = 1 n ( X i - X _ ) 2 / n é um estimador enviesado de σ 2 .

Passo 2

Letra b:

Vamos encontrar a quantidade de tendenciosidade no estimador.

t e n d e n c i o s i d a d e = E ∑ i = 1 n ( X i - X ̄ ) 2 n - σ 2

= - σ 2 n

Passo 3

Letra c:

Conforme o tamanho da amostra n aumenta, a tendenciosidade aumenta.

Resposta

  1. ∑ i = 1 n ( X i - X _ ) 2 / n é um estimador enviesado de σ 2 .
  2. = - σ 2 n
  3. Conforme o tamanho da amostra n aumenta, a tendenciosidade aumenta.
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontrando a média ponderada - Nos exercícios 41 a 46, determine a média ponderada dos dados.43. Saldo de conta - Para o mês de abril, uma conta bancária tem saldo de US$ 523 por 24 dias, US$ 2.415 p
Nota final No Exercício 41, foi cometido um erro no lançamento de sua nota na prova final. Em vez de 93, sua nota foi 85. Qual é a sua nova média ponderada?
Encontrando a média ponderada - Nos exercícios 41 a 46, determine a média ponderada dos dados.45. Graus - Um estudante recebe os seguintes graus, com A valendo 4 pontos, B valendo 3 pontos, C valendo
Encontrando a média de uma distribuição de frequência. Nos exercícios 49 a 52, aproxime a média da distribuição de frequência. 49. Economia de combustível - A distância percorrida na estrada (em milha
Encontrando a média ponderada - Nos exercícios 41 a 46, determine a média ponderada dos dados.46. Notas - As notas médias para estudantes de um curso de estatística (por graduação) são dadas a seguir.