Enunciado
Probabilidade e Estatística - Estatistica Mauri Guerra estatistica indutiva- Ed: 1º - Capítulo 10.Exercícios propostos - Ex. 4
Os pesos de certo produto são: 2,021; 2,005; 2,009; 2,002; 1,990; 1,983; 2,001; 1,990; 1,987 kg. Testar a hipótese de , contra , ao nível de 5%.
Passo 1
Olá galerinha, vamos resolver este exercício de acordo com o passo a passo dos testes de hipóteses.
Então primeiramente iremos definir nossa hipótese nula () e alternativa ():
- ;
- .
O teste é bilateral e como o desvio padrão populacional () é desconhecido, vamos utilizar a variável de Student, com () graus de liberdade.
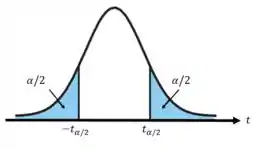
Passo 2
Do enunciado:
- ;
- .
Pela tabela da distribuição :
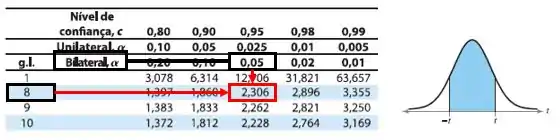
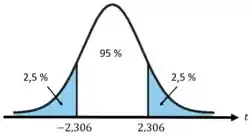
- Se aceita ;
- Se rejeita .
Passo 3
Para calcularmos o valor , primeiramente precisamos do valor da média () e do desvio padrão () amostral, para isso vamos utilizar as equações:
Logo:
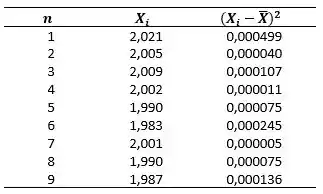
Passo 4
Agora iremos calcular nosso valor , pela seguinte equação:
Sendo que:
- ;
- .
Logo:
Como , então aceitamos .
Tchau galerinha! Te espero em mais exercícios.
Resposta
aceita .