Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 9.Exercícios - Ex. 56
9-56.Reconsidere os dados de Medicine and Science in Sports and
Exercise,deseritos no Exercicio 8-26.0 tamanho da amostra foi igual
a sele e a media e o desvio-padrao da amostra foram 315 We 16 W.
respectivamente.
（a)Ha evilencia de que a resistencia da perna excede 3(0)W.com um
nivel de significancia de 0.05?Encontre o valor P.
（b)Caleule a potencia do teste.se a resisteni veddia for 305 W.
（c)Que tamanho da amosta seria requerido para detectar uma media
verdadeira de 305 W.se quisessemos que a potencia do teste fosse
no minimo 0.90?
（d)Explique como a questao no item(a)poderia ser respondida com Um
intervalo de conlianga.
Passo 1
Sabemos que o desvio padrão , média da amostra e o tamanho da amostra é . O valor P para o contra a alternativa unilateral é a probabilidade acima , ou seja
onde vamos usar a estatística de teste
Passo 2
Letra a:
Precisamos testar
Contra
usando
O teste de estatística é
Sabemos que , então
Se então, falhamos em rejeitar .
Portanto,
e concluímos que não é verdadeiro.
Agora, da Equação (1), obtemos
Da Tabela V do Apêndice nós sabemos
Portanto,
Então, o valor P é
Passo 3
Letra b:
Quando o valor verdadeiro da média é , a distribuição de é chamada de distribuição t não central com grau de liberdade e parâmetro de não centralidade . O erro tipo II da alternativa de dois lados seria
onde denota a variável aleatória t não central, ou seja,
Encontrando a probabilidade de erro do tipo II para o teste t envolve encontrar a probabilidade contida entre dois pontos da distribuição t não central.
Este problema já foi resolvido, e os resultados são resumidos em uma série de curvas nos Gráficos do Apêndice VIIe, VIIf, VIIg e VIIh. As curvas são fornecidas para alternativas bilaterais nos Gráficos VIIe e VIIf. Nesses gráficos, o fator d é definido como
Para a alternativa unilateral ou usamos os gráficos VIIg e VIIh.
Nós vemos que d depende do parâmetro desconhecido . Podemos evitar essa dificuldade de várias maneiras. Em alguns casos, poderíamos usar a variância da amostra para estimar um .
O teste se a verdadeira força é de 305 watts, então
Referindo-nos às curvas características de operação no Apêndice Gráfico VIIe (para ) com e , descobrimos que , aproximadamente.
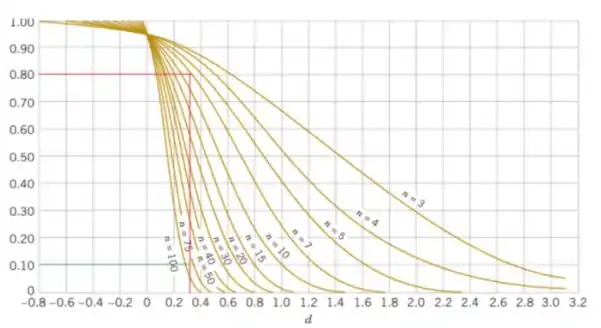
Então, a potência do teste é
Passo 4
Letra d:
Queremos a potência do teste a ser pelo menos e média da amostra verdadeira , então (ver figura anterior, linha verde). Em seguida, vemos que o tamanho da amostra é
Passo 5
Letra e:
Um IC unilateral de na média é
Portanto, um IC unilateral de 95% na média é
Se testarmos
Contra
Então rejeitamos porque 300 não está em um IC de .