Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 4.Problemas - Ex. 3
Numa pesquisa sobre rotatividade de mão-de-obra, para uma amostra de 40 pessoas foram observadas duas variáveis: número de empregos nos últimos dois anos (X) e salário mais recente, em número de salários mínimos (Y). Os resultados foram:
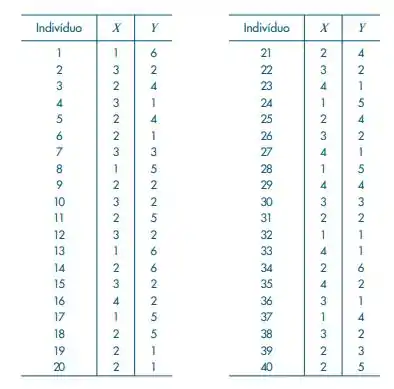
(a) Usando a mediana, classifique os indivíduos em dois níveis, alto e baixo, para cada uma das variáveis, e construa a distribuição de freqüências conjunta das duas classificações.
(b) Qual a porcentagem das pessoas com baixa rotatividade e ganhando pouco?
(c) Qual a porcentagem das pessoas que ganham pouco?
(d) Entre as pessoas com baixa rotatividade, qual a porcentagem das que ganham pouco?
(e) A informação adicional dada em (d) mudou muito a porcentagem observada em (c)? O que isso significa?
Passo 1
Vamos lá!
Primeiro, precisamos calcular a mediana das variáveis X e Y.
Vamos direto ao ponto?
Mediana é o valor central dos dados colocados em ordem não decrescente, certo?
Dessa forma, temos
Agora, vamos construir a distribuição de freqüências conjunta das duas classificações, beleza?
Passo 2
Para descobrirmos se X = alto ou baixo e Y = alto ou baixo, basta vericarmos os pares de valores e verem se eles estão acima ou abaixo das medianas.
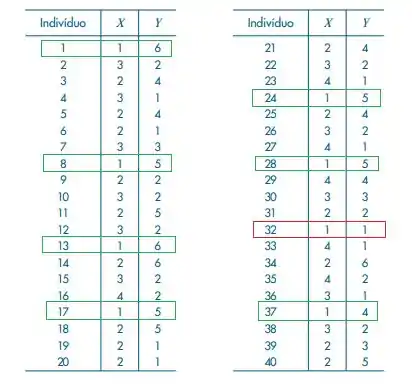
Em vermelho, temos apenas 1 indivíduo: X = baixo e Y = baixo; e em verde 7 indivíduos: X = baixo e Y = alto, certo? Vamos seguir essa ideia para acharmos o número de indivíduos restantes?
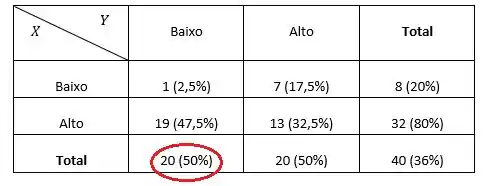
Logo, temos a seguinte distribuição de freqüências conjunta
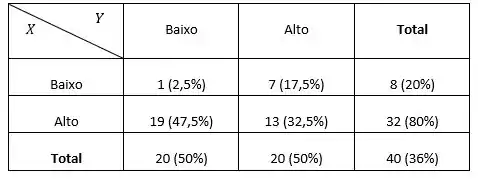
Notem que para ecomonizar tempo, na tabela já se encontram os valores das frequências absolutas e relativas 😉.
Passo 3
(b) Qual a porcentagem das pessoas com baixa rotatividade e ganhando pouco?
Basta olharmos para a nossa tabela.
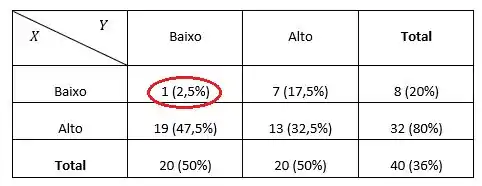
Da tabela, tem-se que 2,5% dos indivíduos encontram-se nessas condições.
Passo 4
(c) Qual a porcentagem das pessoas que ganham pouco?
Passo 5
(d) Entre as pessoas com baixa rotatividade, qual a porcentagem das que ganham pouco?
Opa! Vocês concordam comigo que agora queremos uma probabilidade condicional?
Queremos , certo?
Sabemos que . Trazendo para o nosso problema, temos
Passo 6
(e) A informação adicional dada em (d) mudou muito a porcentagem observada em (c)? O que isso significa?
A probabilidade em (c) foi bastante modificada. Isto indica que a maioria das pessoas que ganham pouco têm rotatividade.
Resposta
(a)
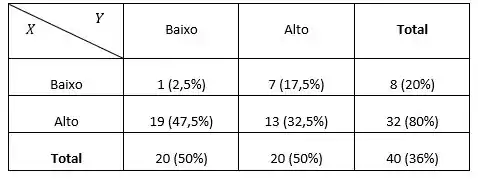
(b) 2,5%
(c) 50%
(d) 12,5%
(e) A probabilidade em (c) foi bastante modificada. Isto indica que a maioria das pessoas que ganham pouco têm rotatividade.