Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 4.Problemas - Ex. 4
Usando os dados do Problema 1, responda:
(a) Qual a distribuição das proporções do grau de educação segundo cada uma das regiões de procedência?
(b) Baseado no resultado anterior e no Problema 2, você diria que existe dependência entre a região de procedência e o nível de educação do funcionário?
Passo 1
Do Problema 1, temos a seguinte distribuição de freqüência conjunta para as variáveis grau de instrução e região de procedência.
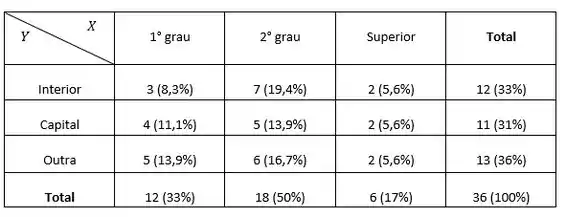
(a) Qual a distribuição das proporções do grau de educação segundo cada uma das regiões de procedência?
Opa! Falou em PROPORÇÃO, a gente lembra de PROBABILIDADE, né? E nesse caso, a probabilidade é dada pela FREQUÊNCIA RELATIVA, certo?
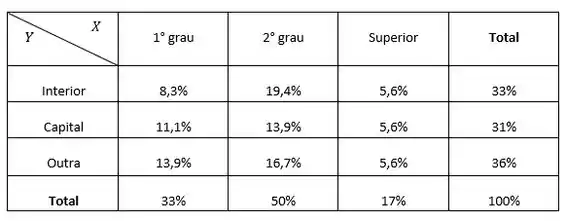
Logo, para construirmos a distribuição das proporções do grau de educação segundo cada uma das regiões de procedência, basta utilizarmos apenas os valores probabilísticos. Dessa forma, temos
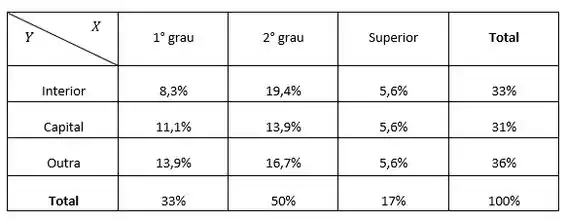
Passo 2
(b) Baseado no resultado anterior e no Problema 2, você diria que existe dependência entre a região de procedência e o nível de educação do funcionário?
Inicialmente, verificamos que fica muito difícil tirar alguma conclusão, devido à diferença entre os totais marginais. Devemos, pois, construir as proporções segundo as linhas ou as colunas para podermos fazer comparações. Fixemos os totais das linhas
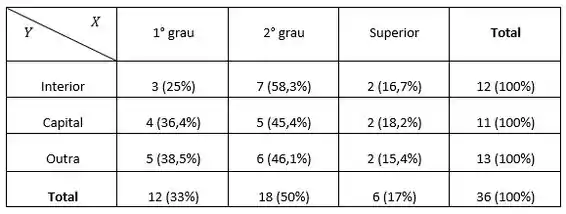
Agora os totais das colunas
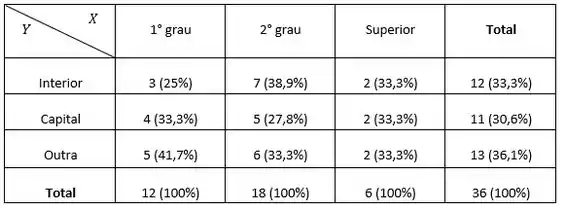
As tabelas acima indicam existência de dependência entre as variáveis região de procedência e grau de escolaridade, pois as proporções marginais não se repetem no interior da tabela.
Resposta
(a)
(b Existe dependência, pois as probabilidades marginais não se repetem no interior da tabela.