Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 8.6 - Ex. 36
Um levantamento inicial sugere que o número de filhos depende da renda familiar dos pais. Para confirmar essa suspeita, amostras de famílias foram coletadas, em cada classe social, e o número de filhos em cada família foi contado. Verifique através de um teste de hipóteses se a variável tem comportamento diferente em cada uma das subpopulações estudadas (use nível de significância de 1%).
Passo 1
Eaai pessoa, vamos pra mais um Teste de homogeneidade, dessa vez o enunciado deixa bem claro que temos uma únical variável:
Sendo estudada em diferentes subpopulações.
Portanto, vamos realiar o teste aproximando pela distribuição Qui-quadrado, dessa forma:
Lembrando, que são os valores observados em cada célula na tabela do enunciado; enquanto que são as linhas (subpopulações) e colunas respectivamente.
E como de praxe vamos ter de obter os valores esperados em cada célula , lembra como faz?
Perceba que o total de amostras em cada população é nada mais que a soma da linha.
Passo 2
Antes de calcular, vamos as nossas hipóteses:
Contra:
Tá comigo? Então bora calcular issodaê:
E assim por diante até:
Depois de calcular tudo, montei a tabelinha a seguir para ficar mais fácil visualizar:
Bateu tudo aí?? Olha só, toma cuidado com as aproximações, a soma desses valores tem de ser o mais próximo possível da soma dos valores dados, ou seja, a soma total dessa tabela tem que ser igual a 360 (ou o mais perto possível).
Agora, antes de relizar o teste com a qui-quadrado, vamos definir a nossa região crítica:
O enunciado deu pra gente o , portanto precisamos buscar um tal que:
Então a gente vai precisar ir na tabela de distribuição qui-quadrado na coluna de 1% e na linha de graus de liberdade.
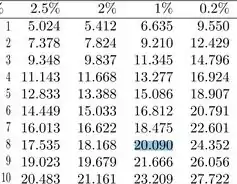
Portanto, encontramos , e aí nossa RC:
Passo 3
Agora, finalmente podemos realizar o teste:
Claramente, pertence e muito à região crítica, então devemos rejeitar a hipótese nula.
Resposta
Concluindo, existem evidências de que o número de filhos por família não é homogêneo nas classes.