O reconhecimento de características dos modelos de superfície de peças complexas está se tomando cada vez mais importante no desenvolvimento de sistemas de projeto auxiliado por computador (computer-aided design - CAD) eficientes. O artigo "A Computationally Efficient Approach to Feature Abstraction in Design-Manufacturing Integration" (J. of Engr: for Industry, 1995, p. 16-27) contém um gráfico de (tempo total de reconhecimento), em que o tempo é apresentado em s, versus (número de bordas de uma peça), do qual foram reproduzidos os seguintes dados representativos:
a. Um gráfico de dispersão de log(tempo) versus log(bordas) indica uma relação linear aproximada entre essas duas variáveis?
b. Que modelo probabilístico para relacionar tempo de reconhecimento número de bordas é subentendido pela relação de regressāo linear simples entre as variáveis transformadas?
c. As quantidades calculadas com base nos dados, são
Calcule as estimativas de parâmetro do modelo na parte (b) e, em seguida, obtenha uma previsão pontual do tempo em relação a um número de bordas de 300 .
Passo 1
E aí pessoal partiu para mais uma questão de (probabilidade)? Abaixo começaremos trazendo algumas informações do enunciado:
Um gráfico de dispersão de log(tempo) versus log(bordas) indica uma relação linear aproximada entre essas duas variáveis?
a.
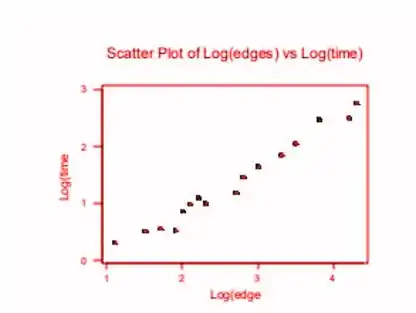
Sim, o gráfico de dispersão das duas variáveis transformadas parece bastante linear e, portanto, sugere uma relação linear entre as duas.
Passo 2
Que modelo probabilístico para relacionar tempo de reconhecimento número de bordas é subentendido pela relação de regressāo linear simples entre as variáveis transformadas?
b. Deixando y denotar a variável 'tempo', o modelo de regressão para as variáveis y' e x' é . Exponenciando (tomando os antilogs de ) ambos os lados dá ; i.e., o modelo é em que e . Este modelo é frequentemente chamado de modelo de regressão de "função de potência"
Passo 3
c. Usando as variáveis transformadas y^' e x^', as somas de quadrados necessárias são e Portanto e . A estimativa de é e . O modelo de função de potência estimado é então . Para , o valor previsto de é , ou sobre segundos.
Resposta
Sim, o gráfico de dispersão das duas variáveis transformadas parece bastante linear e, portanto, sugere uma relação linear entre as duas.
b. Este modelo é frequentemente chamado de modelo de regressão de "função de potência"
c. O modelo de função de potência estimado é então . Para , o valor previsto de é , ou sobre segundos.
Espero que tenham aprendido com essa questão, até a próxima !