Enunciado
Probabilidade e Estatística - Jay Devore, Probabilidade e estatística para engenharia e ciências- Ed: 6º - Capítulo 13.Exercícios Suplementares - Ex. 69
Foram medidas a pressão atmosférica (psi) e a temperatura de um processo de compressāo em um determinado dispositivo de cilindro com êmbolo, gerando os dados a seguir (de Introduction to Engineering Experimentation, Prentice-Hall, Inc., 1996, p. 153):
a. Você ajustaria o modelo de regressão linear simples aos dados e o usaria como base para prever a temperatura de acordo com a pressão? Por quê ou por quê não?
b. Encontre um modelo probabilístico adequado e use o para prever o valor da temperatura resultante de uma pressão de 200 da maneira mais informativa possível.
Passo 1
E aí pessoal partiu para mais uma questão de (probabilidade)? Abaixo começaremos trazendo algumas informações do enunciado:
Você ajustaria o modelo de regressão linear simples aos dados e o usaria como base para prever a temperatura de acordo com a pressão? Por quê ou por quê não?
a. Com base em um gráfico de dispersão (abaixo), um modelo de regressão linear simples não seria apropriado. Por causa da leve, mas óbvia curvatura, um modelo quadrático provavelmente seria mais apropriado.
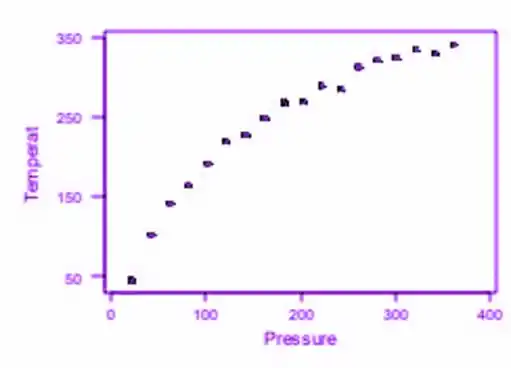
Passo 2
b. Usando um modelo quadrático, uma equação de regressão gerada pelo Minitab é , e uma estimativa pontual de temperatura quando a pressão é 200 é 280,23. O Minitab também gerará um intervalo de previsão de 95% de (256,25.304,22 ). Ou seja, estamos confiantes de que quando a pressão é de 200psi, um único valor de temperatura estará entre 256,25 e ..
Resposta
Por causa da leve, mas óbvia curvatura, um modelo quadrático provavelmente seria mais apropriado.
b. Ou seja, estamos confiantes de que quando a pressão é de 200psi, um único valor de temperatura estará entre 256,25 e ..
Espero que tenham aprendido com essa questão, até a próxima !