Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Walpole - Probabilidade e Estatística para Engenharia e Ciências- Ed: 8º - Capítulo 10.Exercícios - Ex. 97

As respostas a seguir relacionadas ao padrão de vida no momento de uma pesquisa de opinião independente em mil lares versus uma realizada um ano depois, parecem estar de acordo com os resultados de um estudo publicado no periódico Across the Board (junho de 1981):

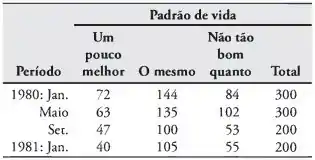
Teste a hipótese de que as proporções de lares em cada categoria de padrão de vida são as mesmas para cada um dos quatro períodos. Use um valor P.

Passo 1

Falaii galerinha do Responde ai, tudo belezinha?

Testar

H 0 : A s   p r o p o r ç õ e s   d e   d o m i c í l i o s   d e n t r o   d e   c a d a   c a t e g o r i a   d e   p a d r ã o   d e   v i d a   s ã o   a s   m e s m a s   p a r a   c a d a   u m   d o s   q u a t r o   p e r í o d o s   d e   t e m p o

H 1   : n e m   t o d a s   a s   p r o p o r ç õ e s   s ã o   i g u a i s

Considere o nível de significância é α   =   0.05

A estatística do teste qui-quadrado é dada como

x 2 = ∑ i = 1 12 f i - e i 2 e i

Sob H 0 a estatística de teste x 2 segue a distribuição de x 2 com ( 4 - 1 ) ( 3 - 1 ) = 6 graus de liberdade, pois há quatro linhas e três colunas.

Passo 2

Vamos considerar a seguinte tabela

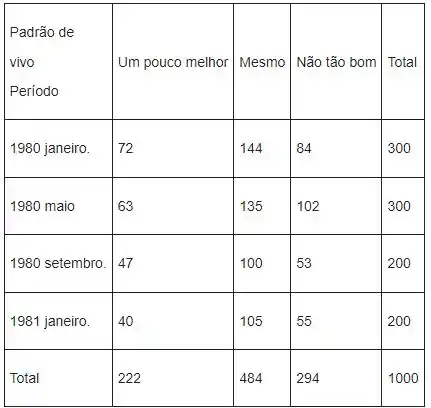
A regra geral para obtenção da frequência esperada de qualquer célula é dada pela seguinte

maneira:

f r e q u ê n c i a   e s p e r a d a = c o l u n a   t o t a l × f i l e i r a   t o t a l t o t a l

Na tabela a seguir, mostraremos a frequência observada junto com a frequência esperada ente colchetes para cada célula

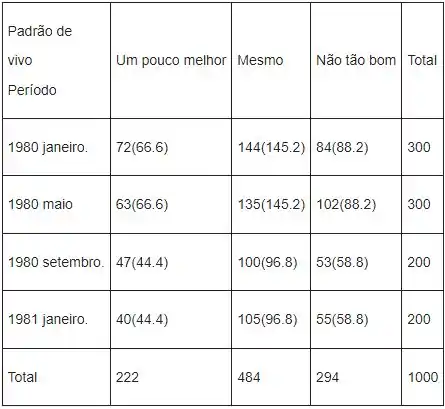
Passo 3

A região crítica é dada como x o b s e r v a d o 2 > x 0.05,6 2 onde x 0.05,6 2 é o ponto 0.05 superior da distribuição x 2 com 6 graus de liberdade.

= 72 - 66.6 2 66.6 + 63 - 66.66 2 66.6 + 47 - 44.4 2 44.4 + 40 - 44.4 2 44.4 + 144 - 145.2 2 145.2 + 135 - 145.2 2 145.2 + 100 - 96.8 2 96.8 + 105 - 96.8 2 96.8 + 84 - 88.2 2 88.2 + 102 - 88.2 2 88.2 + 53 - 58.8 2 58.8 + 55 - 58.8 2 58.8

= 5.924

Passo 4

P - v a l o r = P ( x 2 > 5.924 )

= 1 - P x 2 ≤ 5.924

= 1 - 0.5678

= 0.4322 > 0.05

Como o valor P é maior que o nível de significância, não rejeitamos H 0

O valor calculado qui-quadrado x 2 = 5.924 é menor que o valor critico 12.592

Portanto, não rejeitamos H 0 .

“O coelho está certo, e ele é claramente o mais inteligente entre vocês!”

Resposta

Portanto, não rejeitamos H 0 .

Exercícios de Livros Relacionados

Em um estudo conduzido pelo Centro de Recursos Hídricos e analisado pelo Centro de Consultoria Estatística da Universidade da Virgínia, foram comparadas duas estações de tratamento de esgoto. A estaçã
Em um estudo conduzido pelo departamento de engenharia mecânica e analisado pelo centro de estatística da Universidade da Virgínia, os vergalhões de aço fornecidos por duas empresas diferentes foram c
Numa pesquisa sobre a opinião dos moradores de duas cidades, AeB , com relação a um determinado projeto, obteve-se:Construa um I C para a diferença de proporções de opiniões nas duas cidades.
Uma pesquisa mercadológica sobre fidedignidade a um produto foi realizada em dois anos consecutivos, com duas amostras independentes de 400 donas de casa em cada uma delas. A preferência pela marca em
Um partido afirma que a porcentagem de votos masculinos a seu favor será de 10 % a mais do que a porcentagem de votos femininos. Numa pesquisa feita entre 400 homens, 170 votariam no partido, enquanto