Enunciado
Probabilidade e Estatística - Walpole - Probabilidade e Estatística para Engenharia e Ciências- Ed: 8º - Capítulo 10.Exercícios - Ex. 94
A enfermaria de uma faculdade conduziu um experimento para determinar o grau de alívio fornecido por três remédios antitussígenos. Cada remédio foi testado em 50 estudantes e os seguintes dados foram registrados:
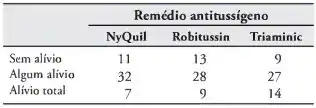
Teste a hipótese de que os três remédios são igualmente eficazes. Use um valor P t m sua conclusão.
Passo 1
Selvaaaaaaaaaa galerinha, isso mesmo selva haha, tudo certinho??
“Hulk esmaga”, Bora esmagar essa questãozinha comigo?
A partir das informações fornecidas, uma enfermaria de faculdade realizou um experimento para determinar o grau de alívio fornecido por três remédios para tosse.
Competir a hipótese nula e alternativa:
Considere o nível de significância é
A estatística do teste qui-quadrado é dada como
Sob a estatística de teste segue a distribuição de com graus de liberdade, pois há três linhas e três colunas.
Passo 2
Vamos considerar a seguinte tabela
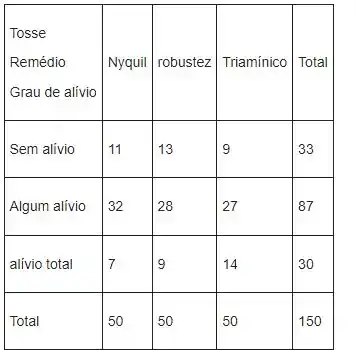
A regra geral para obtenção da frequência esperada de qualquer célula é dada pela seguinte
maneira:
Na tabela a seguir, mostraremos a frequência observada junto com a frequência esperada ente colchetes para cada célula
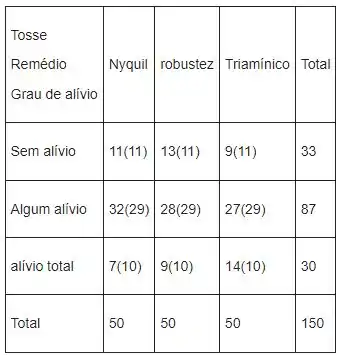
Passo 3
A região crítica é dada como onde é o ponto 0.05 superior da distribuição com 4 graus de liberdade.
Passo 4
O valor de P é maior que o nível de significância , portanto, falha em rejeitar a hipótese nula.
Portanto, há evidencias suficientes de que não há diferenças significativa nos três remédios para tosse.
“OK, isso foi legal.”
Resposta
Portanto, há evidencias suficientes de que não há diferenças significativa nos três remédios para tosse.