Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Walpole - Probabilidade e Estatística para Engenharia e Ciências- Ed: 8º - Capítulo 10.Exercícios - Ex. 113

Em um estudo conduzido pelo Centro de Recursos Hídricos e analisado pelo Centro de Consultoria Estatística da Universidade da Virgínia, foram comparadas duas estações de tratamento de esgoto. A estação A está localizada onde a renda mediana das famílias é abaixo de $ 22.000 por ano. A estação B está localizada onde a renda mediana está acima de $ 60.000 anuais. A quantidade de esgoto tratado em cada estação (milhares de galões/dia) foi amostrada aleatoriamente por dez dias. Os dados estão a seguir:

Podemos concluir, num nível de significância de 5% , que a quantidade média de esgoto tratado na região de alta renda é maior do que a da região de baixa renda? Assuma normalidade

Passo 1

E aí meus queridos? Tudo certinho?

“Operador! Me dê o número do responde ai!.... Preciso resolver essa questão”

Este e um problema de dois exemplos. Seja μ A   e   μ B a verdadeira quantidade média da população de águas residuais tratadas na estação e na estação A, B respectivamente.

Precisamos testar

H 0 : μ A - μ B = 0

H 1 : μ A - μ B > 0

O nível de significância especificado é α = 0.05

Passo 2

Realizamos um teste de duas amostras e a estatística de teste é

t = x A - x B - d 0 s A 2 n A - s B 2 n B

que segue distribuição com v graus de liberdade onde

v = s A 2 n A - s B 2 n B 2 s A 2 n A 2 n A - 1 + s B 2 n B 2 n B - 1

x ¯ A = média amostral para Planta A

x ¯ B = média amostral para Planta B

s A 2 = variação da amostra para a planta

s B 2 = variação da amostra para a planta B

n A   = tamanho da amostra para a planta

n B = tamanho da amostra para a planta

D 0 = diferença das médias populacionais sob Ho

A região crítica é t o b s e r v a d o > t 0.05 ,   v

onde t 0.05 , v , é o ponto superior 0,05 de distribuição t com graus v de liberdade.

Passo 3

Considerando a seguinte tabela

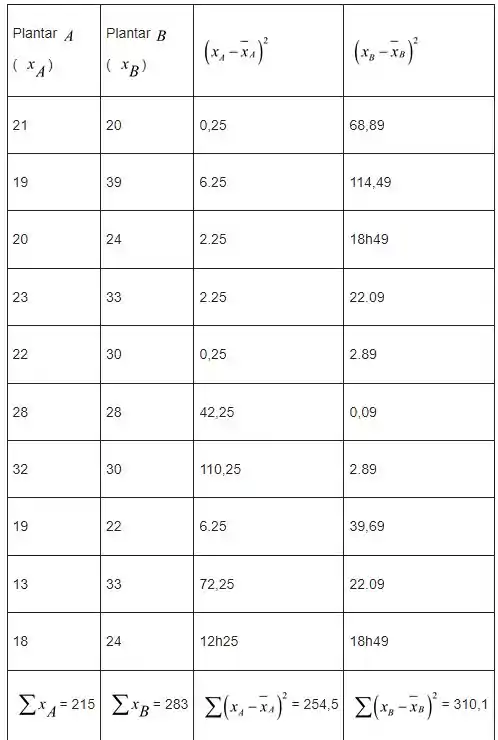
Partindo da tabela

∑ x A = 215

x ¯ A = 1 10 ∑ x A

= 1 10 × 215

x ¯ A = 21.5

∑ x B = 215

x ¯ B = 1 10 ∑ x B

= 1 10 × 2 83

x ¯ B = 2 8.3

s A 2 = 1 10 ∑ x A - x ¯ A 2

= 1 9 × 254.5

= 28.278

s B 2 = 1 10 ∑ x B - x ¯ B 2

= 1 9 × 310.1

= 34.456

n A = n B = 10

t o b s e r v a d a = 21.5 - 28.3 - 0 28.278 10 + 34.456 10

= - 2.71

v = 27.278 10 + 34.456 10 2 28.278 10 2 10 - 1 + 34.456 10 2 10 10 - 1

= 17

Passo 4

O valor tabulado de t 0.05 , 17 = 1.740

Então, t o b s e r v a d o > t 0.05,17 Assim, rejeitamos Hoe concluímos, no 5% nível de significância, que a quantidade média de esgoto tratado no bairro de alta renda é maior do que na área de baixa renda.

"Se algo é difícil de fazer, vale a pena ser feito!"

Resposta

Vide a explicação.

Exercícios de Livros Relacionados

Uma empresa está estudando duas marcas de pneus A e B. Testou 11 pneus de cada marca, quanto a durabilidade, e constatou: para a marca A um média de 23.600 km e um desvio padrão de 3.200 km, e, para a
Se n 1 = 12 , n 2 = 10 , S 1 = 6 , S 2 = 5 , provindas de duas populações normais independentes, testar a hipótese de igualdade das variâncias populacionais, ao nível de 5%.
Numa amostra de 250 elementos verificam-se 24 sucessos e noutra de 100 elementos verificaram-se 15 sucessos. Podemos supor idênticas as probabilidades de sucesso nas duas populações, ao nível de 5%?
Num inquérito com os telespectadores de televisão de uma cidade, 60 de 200 homens desaprovam certo programa, acontecendo o mesmo com 75 de 300 mulheres. Ao nível de 10%, há uma diferença real entre as
Um geneticista está interessado na proporção dehomens e mulheres que tem certo tipo de disfunção sangüínea. Em uma amostra aleatória de cem homens, 31têm a disfunção, enquanto somente 24 de cem mulher