Enunciado
Probabilidade e Estatística - Walpole - Probabilidade e Estatística para Engenharia e Ciências- Ed: 8º - Capítulo 10.Exercícios - Ex. 86
Repita o Exercício 10.83 usando um novo conjunto de dados obtido realizando, de fato, o experimento 64 vezes.
Passo 1
Selvaaaaaaaaaa galerinha, isso mesmo selva haha, tudo certinho??
“Hulk esmaga”, Bora esmagar essa questãozinha comigo?
Para testar se esses dados pertencem a alguma distribuição teórica temos que realizar um teste de qualidade de ajuste
Como a distribuição em questão é , vamos usar para calcular a frequência esperada, calculando as probabilidades para cada número de cartas sorteadas e multiplicando-o pelo número de tentativas.
A tabela de dados empíricos, obtidos através da realização do experimento, tem a seguinte aparência:
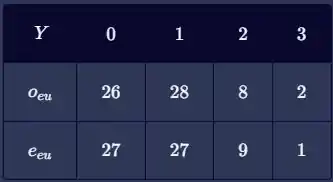
Passo 2
Então, temos que calcular o valor da estatística de teste , que é definido como
Substituindo os valores dados, iremos obter
A região crítica é dada como
Como o valor da estatística de teste não está localizado dentro da região crítica, concluímos que não podemos rejeitar a hipótese nula para aceitar a alternativa, ou seja, podemos assumir que os dados podem ser ajustados em distribuição binomial com esses parâmetros.
“OK, isso foi legal.”
Resposta
Resposta nos passos.