Enunciado
Probabilidade e Estatística - Walpole - Probabilidade e Estatística para Engenharia e Ciências- Ed: 8º - Capítulo 10.Exercícios - Ex. 112
Em um estudo conduzido pelo departamento de engenharia mecânica e analisado pelo centro de estatística da Universidade da Virgínia, os vergalhões de aço fornecidos por duas empresas diferentes foram comparados. Dez amostras de molas foram feitas dos vergalhões fornecidos por cada empresa e a elasticidade foi estudada. Os dados são os seguintes:
Podemos concluir que não há, virtualmente, diferença nas médias entre os vergalhões das duas empresas? Use um valor P para chegar a uma conclusão. As variâncias devem ser combinadas aqui?
Passo 1
Falaiii meus amores, cêis tão suave?
“Se alguma coisa está dificil de ser feita, é porque não é para ser feita" # sóquenão”
Os dados conhecidos para duas empresas são os seguintes:
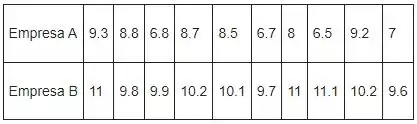
Passo 2
É necessário decidir qual tipo de método é usado para teste t para diferença de duas médias populacionais. Se a razão das variâncias for menor que 2 para as empresas A e B, o teste t agrupado é usado, caso contrário, o teste t não agrupado é aplicável. Primeiro encontre a média amostral e as variâncias padrão amostrais para a empresa A e para a empresa B.
A média amostral para a empresa A é:
A variância da amostra para a empresa A é,
A média amostral para a empresa B é,
A média amostral para a empresa B é,
Passo 3
A razão entre as duas variâncias é simplesmente obtida ela maior variância dividida pela menor variância
Aqui, a proporção de duas variações para a empresa A e a empresa B é maior que 2. Portanto, o teste t não polarizado é usado para testar a afirmação.
Passo 4
As hipóteses nula e alternativa são,
(Sem diferença de média entre as hastes de aço fornecidas pelas duas empresas)
(Diferença de médias entre os vergalhões fornecidos pelas duas empresas)
Aqui, representa as médias populacionais da empresa A e da empresa B.
Sob a hipótese nula, o valor da estatística de teste é,
tem uma distribuição é aproximada com graus de liberdade aproximados. Os graus de liberdade são,
Passo 5
A hipótese alternativa contém símbolo não igual. Portanto, o teste é um teste bicaudal. Agora, é necessário encontrar o valor P bicaudal correspondente ao valor estatístico de teste de
Encontrando o valor P bicaudal
Conclusão: O valor P é menor do que qualquer nível de significância.
Rejeitar a hipótese nula.
Portanto, pode-se concluir que existe diferença de médias entre os vergalhões fornecidos pelas duas empresas.
As variações são agrupadas.
Porque as variações da empresa A e da empresa B não são aproximadamente iguais.
Certo, cérebro, eu não gosto de você e nem você de mim, então faça tudo certo pelo menos uma vez para que eu possa continuar te matando com estudos, certo?
Resposta
Resposta nos passos.