As seguintes pontuações representam as notas no exame final de um curso elementar de estatística:
(a) Construa um diagrama de ramo-e-folhas para as notas, no qual os ramos sejam 1, 2, 3, ..., 9.
(b) Estabeleça uma distribuição de frequências relativas.
(c) Construa um histograma de frequências relativas, desenhe a curva de uma estimativa da distribuição e discuta a assimetria dessa distribuição.
(d) Calcule a média, a mediana e o desvio-padrão amostrais.
Passo 1
Fala galera, beleza? Vamos resolver mais um exercício, vem comigo!
Primeiro vamos expor aqui o diagrama de ramo-e-folhas para as notas, como pedido no item.

Passo 2
Agora vamos ao item b)
Neste item iremos fazer uma tabela com intervalo de classe; ponto médio de classe; frequência e frequência relativa.
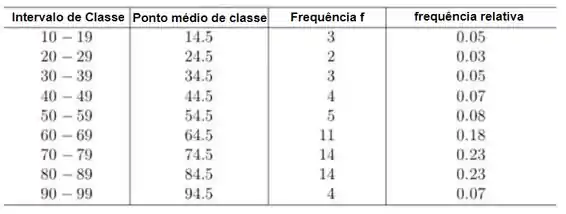
Passo 3
Agora iremos fazer o histograma pedido no item c)
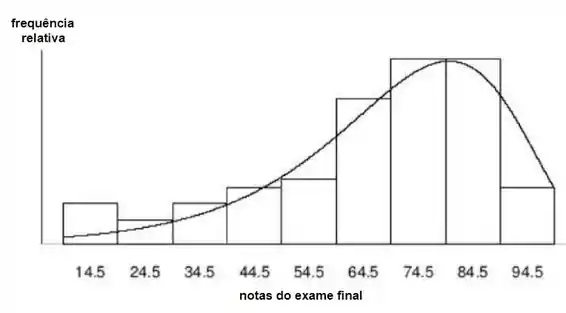
Passo 4
Agora vamos calcular a média, a mediana e o desvio padrão amostrais.
Calculando a média:
Agora organizando os dados em ordem crescente, teremos algo do tipo:
Como , podemos calcular a mediana como:
Usando os termos intermediários encontramos:
Para calcular a variância, temos:
Logo,
Logo,
Resposta
a) vide gráfico.
b) vide gráfico.
c) vide gráfico.
d)