Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 6.3 - Ex. 25f

Seja X tilde N (5,4) . Determine:

(f) P ( - 2 <= X <= - 1 )

Passo 1

Bom, sabemos que se X tilde N ( mu ; sigma^2 ) , podemos usar a seguinte aproximação para a variável:

Z = (X - mu)/(sigma) tilde N ( 0,1 )

Que é a normal padrão.

Então, seja uma probabilidade:

P (a <= X <= b) = P ((a - mu)/(sigma) <= Z <= (b - mu)/(sigma))

É a aproximação pela normal padrão.

Passo 2

Vamos ter o seguinte:

P (- 2 <= X <= - 1) = P ((- 2 - 5)/(2) <= Z <= (- 1 - 5)/(2))

E portanto:

P (- 3,5 <= Z <= - 3)

Lembre-se que na verdade, vamos buscar na tabela o seguinte:

P (0 <= Z <= 3,5) - P ( 0 <= Z <= 3,0 )

Passo 3

Vamos la então:

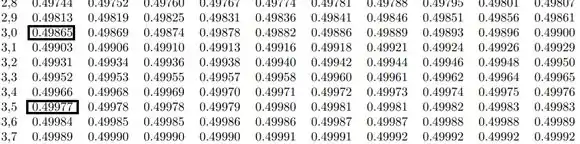
Ou seja,

P (- 3,5 <= Z <= - 3) = 0,49 977 - 0,49865 = 1 , 1 . 10^(- 3)

Resposta

(f) P (- 2 <= X <= - 1) = 0,00 11

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A durabilidade de um tipo de pneu da marca Rodabem é descrita por uma variável aleatória Normal de média 60.000 k m e desvio padrão 8.300 k m .Se a Rodabem garante os pneus pelos primeiros 48.000 k m
A durabilidade de um tipo de pneu da marca Rodabem é descrita por uma variável aleatória Normal de média 60.000 k m e desvio padrão 8.300 k m .O que aconteceria com o item (a) se a garantia fosse para
A durabilidade de um tipo de pneu da marca Rodabem é descrita por uma variável aleatória Normal de média 60.000 k m e desvio padrão 8.300 k m .Se você comprar 4 pneus Rodabem, qual será a probabilidad
A durabilidade de um tipo de pneu da marca Rodabem é descrita por uma variável aleatória Normal de média 60.000 k m e desvio padrão 8.300 k m .(c)Qual deveria ser a garantia (em k m ) de tal forma a a
Sendo X tilde U [ 0,4 ] , calcule:c. P (1X2) .