Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 12.Problemas - Ex. 15a

Sendo X o custo de manutenção de um tear, sabe-se que X ~ N ( μ ; 400 ) . Para testar a

Hipótese H 0 : μ = 200   c o n t r a   H 1 : μ > 200 , será usada uma amostra de 25 teares.

(a) Fixando-se   α   =   5 % , encontre a correspondente RC.

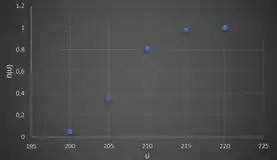
(b) Atribuindo-se valores arbitrários para μ , esboce a função poder do teste.

(c) Para que valores de μ o poder será maior do que 50%?

Passo 1

Temos então: X = c u s t o   d e   m a n u t e n ç ã o   d e   u m   t e a r

Com, X ~ N μ ; 400 .

Do enunciado:

H 0 : μ = 200   c o n t r a   H 1 : μ > 20 0

N = 25   t e a r e s

  1. Com α = 5 % :  

    2. P X - > x c 1 X ~ N μ ; 400 = P X - - μ σ 2 N > x c 1 - μ σ 2 N = p Z > x c 1 - 200 400 25 = 0,05

    Logo:

    x c 1 - 200 400 25 = 1,64 → x c 1 = 206,56

    Passo 2

  2. Lembrando que a função poder é definida da seguinte maneira:

    3. π μ = P r e j e i t a r   H 0 μ = P X - ∈ R C   μ )

    1. P X - > 206,56   μ = 200 ) = P Z > 1,64 = 0,05
    2. P X - > 206,56   μ = 20 5 ) = P Z > 0,39 = 0,34827
    3. P X - > 206,56   μ = 210 = P Z > - 0,86 = 0,805
    4. P X - > 206,56   μ = 21 5 = P Z > - 2,11 = 0,98257
    5. P X - > 206,56   μ = 2 20 = P Z > - 336 = 0,99961

    Passo 3

  3. π μ = P r e j e i t a r   H 0 μ = P X - > 206,56   μ = 0,50

Portanto: P Z > 206,56 - μ 4 = 0,50  

206,56 - μ 4 = 0 →   μ = 206,56

Resposta

  1. R C = X - ∈ R X - > 206,56 }   o u   ] 206,56   ; + ∞ [

  3. π 206,56 = 50 %
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Suponha que estejamos testando H 0 : p = 0,5     c o n t r a   H 1 : p ≠ 0,5   , e que, para uma amostrade tamanho n = 10 , decidimos pela região crítica R C   =   0 ,   1 ,   2 ,   8 ,   9 ,   10 .(b
Seja X uma v.a. com distribuição binomial, c o mn = 15 . Considere: H 0 : p ≥ 0,5 c o n t r a H 1 : p0,5 com R C = 0,1 , 2 . (a) Calcule a probabilidade d oe r r ot i p oI . (b) Calcule a probabilidad
Suponha que estejamos testando H 0 : p = 0,5 c o n t r aH 1 : p ≠ 0,5 , e que, para uma amostrade tamanho n = 10 , decidimos pela região crítica R C={ 0 ,1 ,2 ,8 ,9 ,10 } .(a) Determine o nível de sig