Suponha que apenas 0,10% de todos os computadores de certo tipo apresentem falhas de CPU durante o período de garantia. Considere uma amostra de 10.000 computadores. a. Qual é o valor esperado e o desvio padrão do número de computadores da amostra que apresentam defeito? b. Qual é a probabilidade (aproximada) de mais de 10 computadores da amostra apresentarem defeito? c. Qual é a probabilidade (aproximada) de nenhum computador da amostra apresentar defeito?
Passo 1
- O número de sucessos entre um número fixo de tentativas independentes com uma probabilidade constante de sucesso segue uma distribuição binomial.
- Quando n>50 e np
Assim, é apropriado aproximar a distribuição binomial pela distribuição de Poisson.
Avalie a definição de probabilidade de Poisson em k=0,1,2,3,...,10
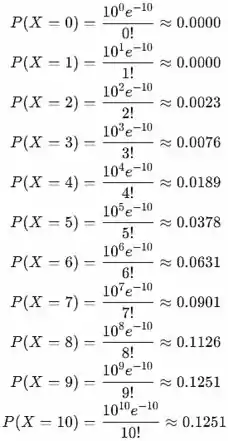
Use a regra de adição para eventos mutuamente exclusivos:
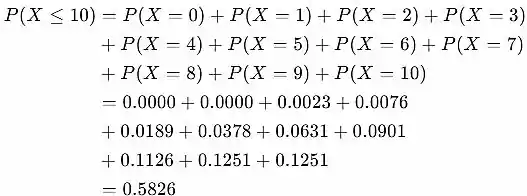
Use a regra do complemento:
Passo 3
- Quando n>50 e np
A média de uma distribuição binomial é o produto do tamanho da amostra n e a probabilidade p
O desvio padrão de uma distribuição binomial é a raiz quadrada do produto do tamanho da amostra n e as probabilidades pp e q. A variância é o quadrado do desvio padrão.
Passo 2
Avalie a definição de probabilidade de Poisson em k=0:
Resposta
Ver o desenvolvimento