Um instrutor que lecionou estatística para engenheiros para duas turmas no semestre passado, a primeira com 20 alunos e a segunda com 30, decidiu pedir aos alunos um projeto semestral. Após a entrega de todos os projetos, o instrutor os organizou aleatoriamente antes de corrigi-los. Considere os primeiros 15 projetos a serem corrigidos. a. Qual é a probabilidade de exatamente 10 projetos serem da segunda turma? b. Qual é a probabilidade de pelo menos 10 projetos serem da segunda turma? c. Qual é a probabilidade de ao menos 10 projetos serem da mesma turma? d. Qual é o valor médio e o desvio padrão do número de projetos entre esses 15 que pertencem à segunda turma? e. Qual é o valor médio e o desvio padrão do número de projetos que não estão entre os 15 primeiros que pertencem à segunda turma?
Passo 1
- Dado
- Adicione as probabilidades correspondentes usando a distribuição hipergeométrica:
- Sabemos também que precisamos incluir a probabilidade de que pelo menos 10 se originem da primeira seção (r=20 em vez de r=30).
- A média da distribuição hipergeométrica é
- A distribuição do número de projetos NÃO da segunda seção usa r=20r=20 (primeira seção) em vez de r=30 (segunda seção).
Definição de distribuição hipergeométrica:
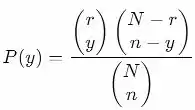
Para y = 10
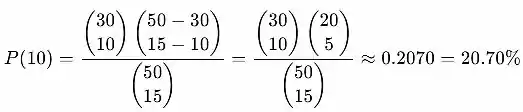
Passo 2
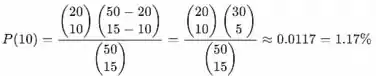
Adicione as probabilidades correspondentes usando a distribuição hipergeométrica:
Adicione esta probabilidade à probabilidade encontrada na parte b
Passo 3
O desvio padrão da distribuição hipergeométrica é:
![]()
A média da distribuição hipergeométrica é:
O desvio padrão da distribuição hipergeométrica é:
![]()
Resposta
Ver o desenvolvimento