Suponha que duas cartas sejam tiradas ao acaso de um baralho de cartas. Seja X o número de azes obtido e seja Y o número de damas obtido.
Estabeleça a distribuição de probabilidade conjunta de (X,Y), as distribuições marginais e as distribuições condicionadas.
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para encontrarmos as probabilidades e distribuições. Parece muita coisa, mas é tranquilo. Partiu??
Passo 2
Ok, nosso primeiro passo vai ser relembrar o que o exercício nos deu. Preparado??
Com essa estrutura de probabilidade, podemos arrumar para botar em função do primeiro valor da distribuição dela. Lembra como faz?? Não?? Vai lá na teoria que eu te esperoaqui...
Achou?? Então me diz aii...
Substituindo nossos valores ali, vamos montar uma tabela para nos ajudar. Nela, vamos botar as probabilidades de saírem só azes, só damas e a soma para cada uma das opções.
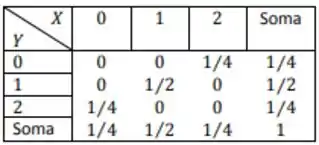
Passo 3
Pronto!! Agora é só obter nossa distribuição!!
Resposta
Ei, a resposta está no passo a passo :)