Exercícios de Teorema Central do Limite - Lista de Exercícios Resolvida

Um pequeno restaurante tem uma receita diária - da qual já foi descontado o gasto com ingredientes - cuja média é de 800 reais e cujo desvio padrão é de 300 reais. A despesa mensal do restaurante com mão de obra, encargos, manutenção, etc., é da ordem de 12.000 reais.

1. Se ele funciona na base de 25 dias por mês, qual a probabilidade de que esse negócio dê um lucro de pelo menos 7.000 reais por mês?
2. Digamos que, em um determinado mês, o restaurante só vai ficar aberto durante 20 dias. Mas, ainda assim, deseja-se manter a meta de um lucro mínimo de 7.000 reais. Para quanto deveria aumentar a média da receita diária para que nesse mês, uma vez mantido o desvio padrão da receita diária em 300 reais, essa meta fosse atingida com probabilidade 95%?

Obs.: Admita que em ambos os casos o tamanho amostral é suficientemente grande para que seja válida a aproximação fornecida pelo Teorema Central do Limite.

e representam os valores (em reais) que as ações A1 e A2, respectivamente, terão daqui a um ano. Como sabemos, o comportamento caótico da bolsa de valores implica que e podem ser considerados aleatórios. Suponha, mais especificamente, que:

1. é modelada por uma distribuição Normal com média de 30 reais e variância de 100 reais²;
2. é modelada por uma distribuição Normal com média de 60 reais e variância de 400 reais²; e
3. as cotações dessas duas ações são independentes.

Um investidor comprou hoje 300 ações A1 a 25 reais cada uma, e 200 ações A2 a 40 reais cada uma.

1. Quais são a distribuição, a esperança e o desvio padrão do valor total que a carteira de ações deste investidor terá dentro de um ano?
2. Qual é a probabilidade de que essa a carteira de ações tenha se valorizado em pelo menos 50% depois de um ano?

b) Seja uma sequência de v.a.’s independentes com distribuição . Se , quem é a distribuição de ? E da v.a. .

Uma instituição de caridade deseja realizar uma obra que custa em sua sede. Entre os contribuintes habituais dessa instituição, cada um pode contribuir com algo em torno de um desvio padrão de . Se 30 dessas pessoas se quotizarem para levantar fundos com essa finalidade, qual a probabilidade de que eles consigam o montante necessário?

Uma companhia de seguros emitiu apólices para 10000 pessoas, todas da mesma faixa etária. A probabilidade de morte durante um ano é de 0,006 para cada pessoa nessa faixa etária. Em um dia pré-fixado, todos os segurados depositam 12 u.m. e, se algum deles morrer dentro de 1 ano, seus beneficiários receberão 1000 u.m. da seguradora. Qual a probabilidade de que em 1 ano:

(a) A companhia tenha prejuízo?

O tempo de vida de uma lâmpada tem distribuição normal com esperança desconhecida , e um desvio padrão de horas. O valor real de um lote de lampadas e de reais, ou seja, o valor real é reais. Um possível comprador retira uma amostra de lampadas e compra o lote por reais, onde e a média aritmética das vidas das lâmpadas da amostra. Ou seja, o comprador paga reais pelo lote. Qual o menor tamanho da amostra para que haja uma probabilidade de pelo menos do comprador não pagar reais nem a mais nem a menos do valor real?

Túlio está vendendo cartelas de rifa com o objetivo de juntar dinheiro para comprar um vídeo game que custa . Cada cartela de rifa tem um preço aleatório, definido por raspadinhas no corpo da cartela. Em média, compradores pagam com desvio padrão de .

1. Túlio vendeu cartelas. Qual é a probabilidade de ele ter conseguido uma quantia suficiente para fazer a compra que deseja?
2. Quantas cartelas Túlio precisaria vender para conseguir recursos suficientes para essa compra com de probabilidade?

Obs.: Admita que, em ambos os casos, o tamanho amostral é suficientemente grande para que seja válida a aproximação fornecida pelo Teorema Central do Limite.

A quantidade de partículas emitidas por uma fonte radioativa durante um período de uma hora é uma variável aleatória de Poisson com parâmetro λ, a princípio desconhecido. Sabe-se que a probabilidade de nenhuma partícula ser emitida durante esse intervalo de tempo é de 0,00673.

(a) Em média, quantas partículas são emitidas por hora? Escreva também a expressão da função densidade de probabilidade de, o tempo em horas entre duas emissões consecutivas.

(b) Sabendo que em 20 minutos após uma emissão nenhuma outra partícula foi emitida, qual a probabilidade de que precisamos esperar mais meia hora pela próxima emissão?

(c) Sejam os números de partículas emitidas pela fonte ao longo das 24 horas de um determinado dia, e admita que as quantidades de partículas emitidas em horas distintas são independentes entre si. Qual é a probabilidade de, ao longo dessas 24 horas, observarmos a emissão de no máximo 100 partículas?

Um estudo de uma escola particular de ensino médio constatou que as pontuações de seus alunos na prova de “Linguagem, códigos e suas tecnologias” do Enem são normalmente distribuídas com uma média de e uma variância de . As pontuações de seus alunos na prova “Matemática e suas tecnologias” são normalmente distribuídas com uma média de e uma variância de . Dois alunos dessa escola foram selecionados aleatoriamente. Considere que é uma variável aleatória que indica a pontuação na prova de Linguagem do primeiro aluno e a pontuação da prova de Matemática do segundo aluno. Suponha que são independentes. A probabilidade vale:

A distribuição do peso dos usuários de um elevador pode ser modelada por uma Normal com média e com desvio padrão . Suponha que cinco pessoas apareçam aleatoriamente para usar esse elevador. Obs: O limite de carga do elevador é de .

(c) Suponha agora que este elevador será usado para transportar carga de pacotes. A distribuição do peso de cada pacote, sendo todos provenientes do mesmo fornecedor, não pode ser modelado pela Normal. Sabe-se que os pacotes têm em média e desvio padrão . Calcular a probabilidade de que o peso no elevador exceda esse limite.

Os lucros diários de determinado comerciante com a venda de um de seus produtos podem ser considerados variáveis aleatórias independentes. Suponha que o valor médio e o desvio padrão dos lucros diários sejam de respectivamente e . Usando a aproximação fornecida pelo Teorema Central do Limite, calcule:

(a) A probabilidade do lucro trimestral(90 dias) ser superior a .

(b) O lucro semestral (180 dias) máximo a ser garantido com de chance.

(c) Qual o número mínimo de dias necessários para garantir um lucro de pelo menos ,00 com de chance.

Dizemos que a média de uma característica de interesse de um processo em uma linha de produção está “em controle” se a média aritmética de medições desta característica cai entre os limites inferior e superior pré-estabelecidos pelo fabricante. Caso contrário dizemos que está “fora de controle". Desejamos estudar o processo de produção de filamentos de lâmpadas em uma linha de produção através de suas espessuras. Suponha que as espessuras na linha de produção possuam uma média de 148 mícrons e desvio-padrão de 15 mícrons. Foi obtida uma amostra com 25 medições dessas espessuras, e admita que os limites inferior e superior de controle são iguais a, respectivamente, 142 e 156 mícrons.

(a) Qual a probabilidade do processo estar fora de controle? Que suposições foram utilizadas?

(b) Se a probabilidade do processo estar em controle fosse igual a 0, 95, quais seriam os novos limites superior e inferior de controle supondo que são simétricos em torno da média do processo?

Observação: Admita que n=25 pode ser considerado suficientemente grande para que se possa usar o Teorema Central do Limite.

Um pequeno restaurante tem uma receita diária - da qual já foi descontado o gasto com ingredientes - cuja média é de 800 reais e cujo desvio padrão é de 300 reais. A despesa mensal do restaurante com mão de obra, encargos, manutenção, etc., é da ordem de 12.000 reais.

1. Se ele funciona na base de 25 dias por mês, qual a probabilidade de que esse negócio dê um lucro de pelo menos 7.000 reais por mês?
2. Digamos que, em um determinado mês, o restaurante só vai ficar aberto durante 20 dias. Mas, ainda assim, deseja-se manter a meta de um lucro mínimo de 7.000 reais. Para quanto deveria aumentar a média da receita diária para que nesse mês, uma vez mantido o desvio padrão da receita diária em 300 reais, essa meta fosse atingida com probabilidade 95%?

Obs.: Admita que em ambos os casos o tamanho amostral é suficientemente grande para que seja válida a aproximação fornecida pelo Teorema Central do Limite.

Duas marcas de capacitor tem o mesmo custo unitário, apresentando distribuição normal das capacitâncias. A marca ABC tem capacitância media de (mili Farad) e desvio padrão de A marca GHI tem capacitancia media de (mili Farad) e desvio padrão de . Sua indústria utiliza um número elevado destes capacitores. Se o valor mínimo desejável para a capacitancia for m, para que valores de m (em mF) é preferível empregar a marca ABC?

Seja uma variável aleatória discreta distribuida conforme a distribuição de Poisson. Seja a variável aleatória binomial usada na "aproximação da Poisson pela Binomial". Nesse contexto, considere as seguintes afirmações.

a) .

b)

c) .

Quais alternativas são corretas?

Uma moeda honesta é jogada vezes. A probabilidade de se obter entre caras é:

Toda manhã um engenheiro retira cem peças aleatoriamente de um novo lote produzido independentemente dos demais lotes, e verifica quantas peças tem defeito. O número de peças com defeito no dia é indicado por . Sabe-se que a probabilidade de defeito em uma peça é . Ao fim de um período de dias, qual a probabilidade que o número total de peças com defeito seja maior ou igual a ?

A cada ano, alunos ingressam em um determinado curso universitário; sabe-se, com base em dados coletados ao longo dos anos, que metade dos ingressantes conclui o curso. A probabilidade de que pelo menos dos alunos que ingressam anualmente terminem o curso é:

14) A variável aleatória é obtida a partir da soma de variáveis aleatórias independentes, todas com distribuição uniforme em (ou seja, . Y=Uma aproximação para a função densidade de probabilidade de é mostrada na figura ao lado. Os valores de e são respectivamente iguais a:

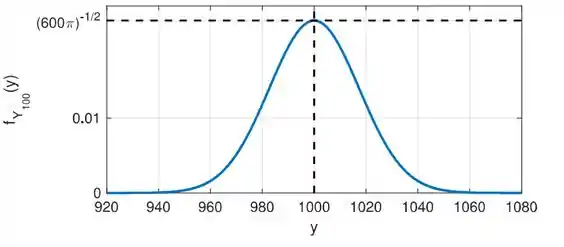
a) e

b) e

c) e

d) e

e) e