Suponha que realizemos um experimento e os resultados possíveis sejam w1, w2, w3, w4, w5.
Definamos as v.a. X e Y cujos valores em cada ponto são dados na tabela a seguir.
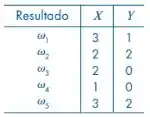
Obtenha as distribuições de probabilidades de X, Y, X + Y, X – Y – 1 e X – Y, supondo que os cinco resultados tenham a mesma probabilidade. Faça um diagrama de dispersão para as variáveis X e Y. Idem para X e X + Y.
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para pegar o que aconteceu lá na combinação das variáveis e encontrar a probabilidade do evento e montar uma tabelinha para cada. Parece muita coisa, mas é tranquilo. Partiu??
Passo 2
Ok, nosso primeiro passo vai ser montar a tabela de distribuição para os eventos.
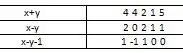
Agora, vamos analisar a distribuição.

Passo 3
Pronto!! Agora é só montar a tabela para cada um dos eventos!!
![]()
![]()
![]()
Resposta
![]()
![]()
![]()