Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 3.Exercícios - Ex. 99
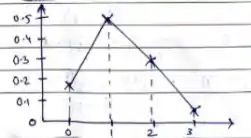
Suponha que tenha uma distribuição hipergeométrica com e . Esquematize a função de probabilidade de . Determine a função de distribuição cumulativa para
Passo 1
Aqui nós temos
A partir daí, vamos achar as probabilidades para cada :
Passo 2
Passo 3
Agora, vamos achar a função de distribuição cumulativa:
Passo 4
E aqui, nós temos o gráfico para a função de probabilidade
Resposta
Exercícios de Livros Relacionados
Suponha que X seja uniformemente distribuída sobre - α ,α , onde α0 . Quando possível, determine α de modo que as seguintes relações sejam satisfeitas:. f x = 1 b - a = 1 2 a F X = x + a 2 a P | X |1
Seja X a duração da vida (medida em horas) de um dispositivo eletrônico. Suponha que X seja variável aleatória contínua com fdp f x = k x n ,2000 ≤ x ≤ 10000 . P a r an = 3 ,d e t e r m i n ek .
Suponha que X seja uniformemente distribuída sobre - α ,α , onde α0 . Quando possível, determine α de modo que as seguintes relações sejam satisfeitas:. f x = 1 b - a = 1 2 a F X = x + a 2 a P X1 2 =
Suponha que X seja uniformemente distribuída sobre - α ,α , onde α0 . Quando possível, determine α de modo que as seguintes relações sejam satisfeitas:. f x = 1 b - a = 1 2 a F X = x + a 2 a P x1 = 1
Seja X uma variável aleatória com distribuição binomial, baseada em 10 repetições de um experimento. Se p=0,3, calcule as seguintes probabilidades, empregando a tábua da distribuição binomial do Apênd