Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 4.Exercícios - Ex. 43
Suponha que tenha uma distribuição normal padrão. Use a Tabela III do Apêndice para determinar o valor de que resolve cada um dos seguintes itens:
Passo 1
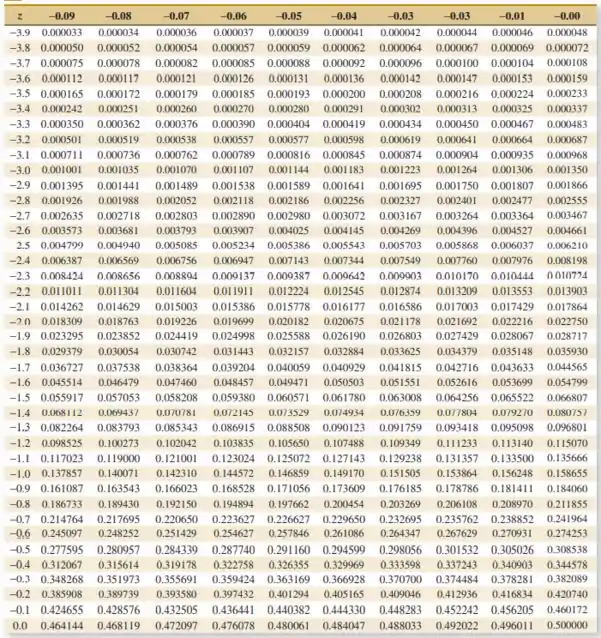
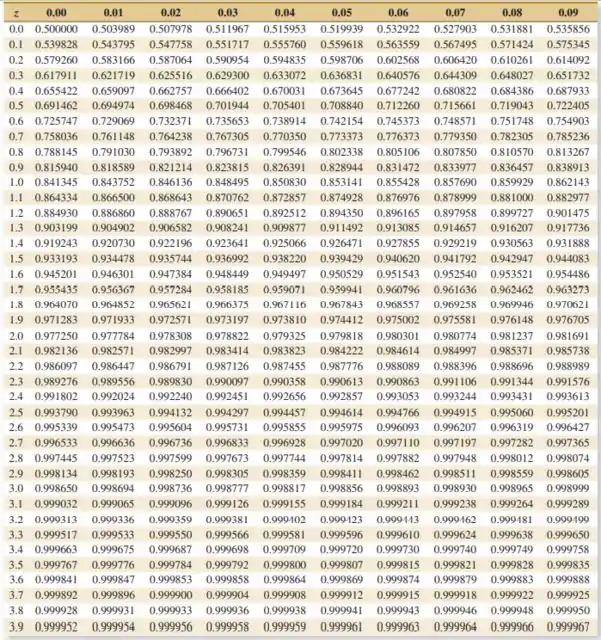
A Tabela III contém as probabilidades à esquerda de ou menores que .
Letra a:
A probabilidade à esquerda de é dada como .
O valor correspondente é então o valor no título da coluna/linha da tabela III que tem a probabilidade mais próxima de 0.9:
Passo 2
Letra b:
A probabilidade à esquerda de z é dada como 0.5. O valor correspondente é então o valor no título da coluna/linha da tabela III que tem a probabilidade mais próxima de 0.5:
Note que a distribuição normal padrão é simétrica em torno de 0 e, portanto, tem uma probabilidade de 0.5 em ambos os lados de .
Passo 3
Na letra c:
A probabilidade à direita de é dada como 0.1, então a probabilidade à esquerda deé (uma vez que a probabilidade total tem que ser igual a 1).
O valor correspondente é então o valor no título da coluna/linha de tabela III que tem a probabilidade mais próxima de 0.9:
Passo 4
Na letra d:
A probabilidade à direita de é dada como 0.9, então a probabilidade à esquerda de é (uma vez que a probabilidade total tem que ser igual a 1).
O valor correspondente é o valor no título da coluna/linha da tabela III que tem a probabilidade mais próxima de 0.1:
Passo 5
Letra e:
A probabilidade dada é:
Reescreva a probabilidade:
Avalie a probabilidade conhecida usando a tabela III:
Adicione 0.107488 a cada lado:
O valor correspondente é então o valor no título da coluna/linha da tabela III que tem a probabilidade mais próxima de 0.107488:
Passo 6
Resposta
- 1.28
- 0
- 1.28
- -1.28
- 1.33