Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 5.Problemas - Ex. 3
Três jogadores A, B e C disputam um torneio de tênis. Inicialmente, A joga com B e o vencedor joga com C, e assim por diante. O torneio termina quando um jogador ganha duas vezes em seguida ou quando são disputadas, ao todo, quatro partidas. Quais são os resultados possíveis do torneio?
Passo 1
Primeiro, vamos começar entendendo o Problema 3.
Considere o organograma: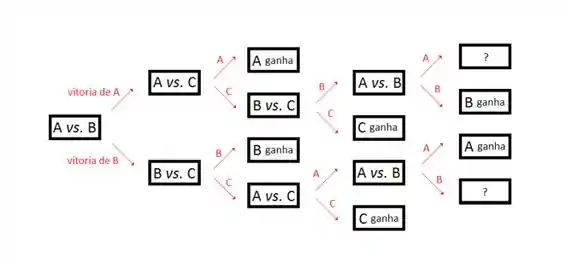 
Para o torneio terminar duas coisas podem acontecer:
(i) Um jogador ganhar duas vezes em seguida
(ii) Quando são disputadas, ao todo, quatro partidas.
Vamos analisar o caso (i) e escrever os possíveis eventos:
(AA) O jogador A ganhou a primeira partida contra B e a segunda contra C.
(BB) Análogo ao caso AA. O jogador B ganhou a primeira partida contra A e a segunda contra C.
(ACC) O jogador A ganhou a primeira partida contra B, mas perdeu a segunda contra C. Já C, ganhou a segunda partida contra A e a terceira contra B.
(BCC) Análogo ao caso ACC.
(ACBB) O jogador A ganhou a primeira partida contra B, mas perdeu a segunda contra C (que foi o vitorioso). Contudo, C perdeu a terceira partida contra B, que foi o vitorioso. B que por sua vez ganhou a terceira partida, também ganhou a quarta contra A.
(BCAA) Análogo ao caso ACBB.
Passo 2
Agora vamos analisar o caso (ii) e escrever os possíveis eventos:
(ACBB) O jogador A ganhou a primeira partida contra B, mas perdeu a segunda contra C (que foi o vitorioso). Contudo, C perdeu a terceira partida contra B, que foi o vitorioso. B que por sua vez ganhou a terceira partida, também ganhou a quarta contra A.
(BCAA) Análogo ao caso ACBB.
(ACBA) O jogador A ganhou a primeira partida B, mas perdeu a segunda contra C (que foi o vitorioso). Contudo, C perdeu a terceira partida contra B, que foi o vitorioso. B que por sua vez ganhou a terceira partida, perde a quarta contra A.
(BCAB) O jogador B ganhou a primeira partida A, mas perdeu a segunda contra C (que foi o vitorioso). Contudo, C perdeu a terceira partida contra A, que foi o vitorioso. A que por sua vez ganhou a terceira partida, perde a quarta contra B.
Passo 3
Fazendo a união dos possíveis resultados de cada caso, temos o seguinte espaço amostral