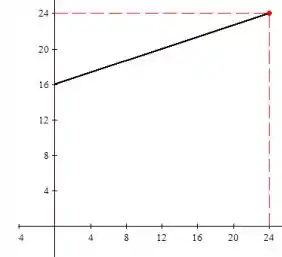
Durante um período de 24 horas, em algum momento x, uma chave é posta na posição “ligada”. Depois, em algum momento futuro y (ainda durante o mesmo período de 24 horas) a chave é virada para a posição “desligada”. Suponha que X e Y sejam medidas em horas, no eixo dos tempos, com o início do período na origem da escala. O resultado do experimento é constituído pelo par de números (X,Y). Descreva o espaço amostral e marque no plano XY os seguintes eventos:
i) O circuito está ligado por uma hora ou menosii) O circuito está ligado no tempo , onde é algum instante no período de 24 horas.iii) O circuito é ligado antes do tempo e desligado no tempo (onde também são dois instantes durante o período de 24 horas especificado).iv) O circuito permanece ligado duas vezes mais tempo do que desligado.
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para encontrarmos o espaço onde vamos achar esses eventos. Parece muita coisa, mas é tranquilo. Partiu??
Passo 2
Ok, nosso primeiro passo vai ser relembrar o que o exercício nos deu. Preparado??
Com esses valores, sabemos que podemos criar um espaço amostral com todas as possibilidades entre esses números.Dessa forma, podemos escrever do seguinte jeito:
Substituindo nossos valores ali, teremos:
Com esse espaço amostral já definido, vamos analisar os eventos que ele pediu.
Para o evento 1, temos que
Então, podemos reesrever da seguinte forma:
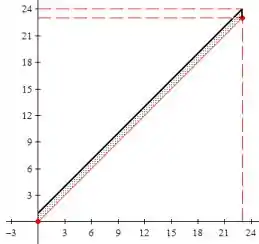
No evento 2, conseguimos a seguinte relação:
Assim, vamos escrever nossa relação como sendo:
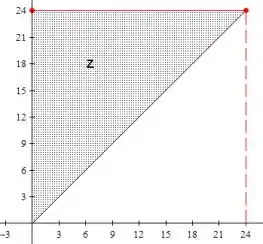
Passo 3
Pronto!! Agora é só obter nossa distribuição!!
Na 3, o circuito é ligado antes do tempo t1 e desligado no t2. Isso nos mostra que:
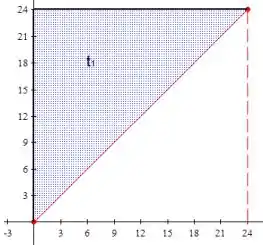
Na distribuição 4, o circuito vai ficar desligado por um tempo D e ligado por um tempo L, o que nos leva a: