Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 5.Problemas - Ex. 11
Dentre seis números positivos e oito negativos, dois números são escolhidos ao acaso (sem reposição) e multiplicados. Qual a probabilidade de que o produto seja positivo?
Passo 1
Vamos lá... Primeira coisa, o que queremos?
Queremos escolher dois números ao acaso e ter como produto desses números um número positivo, certo?
Sabemos que:
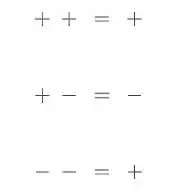
Então, queremos o primeiro e o terceiro caso 😉
Passo 2
Primeiro caso: ambos os números positivos são positivos.
Concordam que olhando para a multiplicação não importa a ordem dos números, basta que ambos sejam positivos, certo? Afinal, a ordem dos fatores não altera o resultado, né? Então usaremos essa combinação!
Evento A: Escolha de dois números positivos ENTRE os seis números positivos.
Espaço amostral: Dado todos os 14 números, dois são escolhidos.
Sabemos que
Passo 3
Segundo caso: ambos os números são negativos.
Evento B: Escolha de dois números negativos ENTRE os oito números negativos.
Espaço Amostral: Dado todos os 14 números, dois são escolhidos.
Sabemos que
Para calcular a probabilidade de obter um resultado positivo, basta somar os dois casos: