Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 8.Problemas - Ex. 8

Numa urna têm-se cinco bolas marcadas com os seguintes números: –1, 0, 0, 0, 1. Retiram-se três bolas, simultaneamente; X indica a soma dos números extraídos e Y o maior valor da trinca. Calcule:

(a) Função de probabilidade de (X, Y).

(b) E(X) e Var(X).

(c) Var(X + Y).

Passo 1

(a) Calcule a função de probabilidade de (X, Y).

A primeira coisa que iremos fazer é montar a tabela de distribuição tanto de X quanto de Y, beleza?

  • X: Indica a soma dos números extraídos:

    • Extraímos 3 bolas simultaneamente, portanto temos

    5 3 = 5 ! 3 ! 2 ! = 10   p o s s i b i l i d a d e s

    Nosso espaço amostral será:

    Assim, a tabela será:

  • Y: O maior valor da trinca

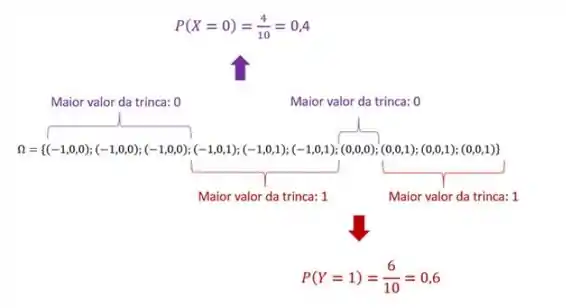
Assim, a tabela será:

Passo 2

Montando a tabela, temos:

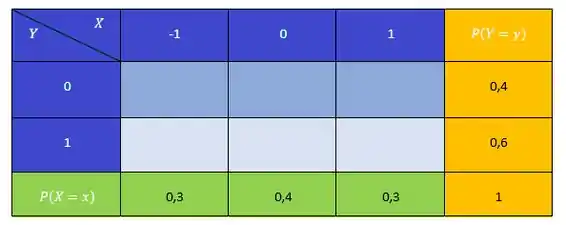
Para preencher o meio da tabela, precisamos olhar novamente para o espaço amostral:

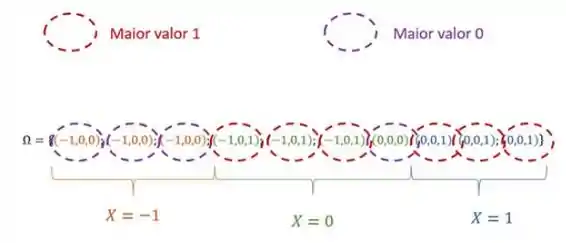
Assim, temos que:

P X = - 1 ,   Y = 0 = 3 10 = 0,3

P X = 0 ,   Y = 0 = 1 10 = 0,1

P X = 1 ,   Y = 0 = 0

P X = - 1 ,   Y = 1 = 0

P X = 0 ,   Y = 1 = 3 10 = 0,3

P X = 1 ,   Y = 1 = 3 10 = 0,3

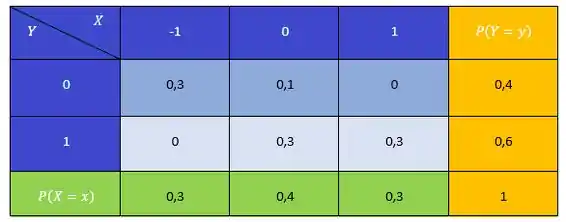
Completando a tabela, temos:

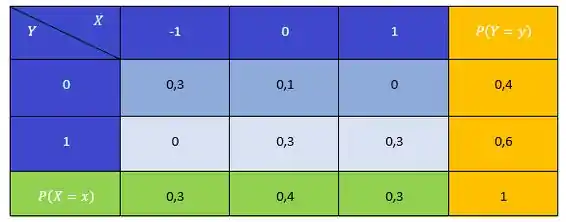
Passo 3

(b) Calcule E(X) e Var(X).

Sabemos que

E X = ∑ i = 1 n x i . P ( X = x i )

Portanto

E X = ∑ i = - 1 1 x i . P X = x i = - 1 . 0,3 + 0 . 0 , 4 + 1 . 0,3 = 0

Para o cálculo da V a r ( X ) precisamos lembrar da seguinte fórmula:

V a r X = E X 2 - E X 2

Portanto, precisamos calcular E ( X 2 )

E X 2 = - 1 2 . 0,3 + 0 2 . 0 , 4 + 1 2 . 0,3 = 0,6

Substituindo nas fórmulas, temos:

V a r X = 0,6 - 0 2 = 0,6

Passo 4

(c) Calcule (c) Var(X + Y).

X   e Y não são independentes, logo:

E X + Y = - 1 0,3 + 0 0,1 + 1 0,3 + 2 0,3 = 0,6

E X + Y 2 = - 1 2 0,3 + 0 2 0,1 + 1 2 0 , 3 + 2 2 0,3 = 1,8

V a r X + Y = 1,8 - 0,6 2 = 1,44

Resposta

(a)

(b) E X = 0                                         V a r X = 0,6

(c) V a r X + Y = 1,44

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Se a variável aleatória X tiver uma fgm dada por M x t = 3 3 - t Qual será o desvio padrão?
Estabeleça a fgm de uma variável aleatória que seja uniformemente distribuída sobre (-1, 2).
Um determinado processo industrial produz grande número de cilindros de aço, cujos comprimentos são distribuídos, normalmente, com média 3,25 polegadas e desvio-padrão 0,05 polegadas. Se dois desses c
Estabeleça a fgm de uma variável aleatória que tenha distribuição geométrica. Essa distribuição possui a propriedade aditiva?
Se X e Y tiverem uma distribuição normal de variada, com função densidade de probabilidade conjunta, mostre que a distribuição de probabilidades marginais de X é normal, com média e desvio padrão. Sug