Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 8.Problemas - Ex. 7d
(d) Como seriam as respostas anteriores se a primeira tira de papel não fosse devolvida à urna antes da segunda extração?
Passo 1
(d) Como seriam as respostas anteriores se a primeira tira de papel não fosse devolvida à urna antes da segunda extração?
A primeira coisa que devemos fazer é determinar o espaço amostral, agora estamos fazendo o experimento SEM reposição, portanto temos:
Passo 2
Analisando apenas a probabilidade da primeira retirada :
Como temos 5 possibilidades (1, 3, 5, 5, 7), podemos afirmar que
Como na urna tem duas tiras de papel do número 5, temos
Montando a tabela de distribuição marginal de
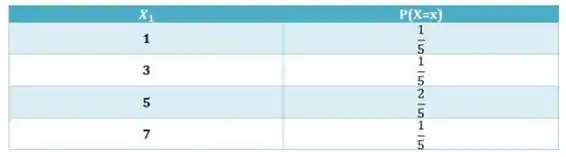
Passo 3
Analisando apenas a probabilidade da segunda retirada :
Como temos 5 possibilidades (1, 3, 5, 5, 7), podemos afirmar que
Como na urna tem duas tiras de papel do número 5, temos
Montando a tabela de distribuição marginal de
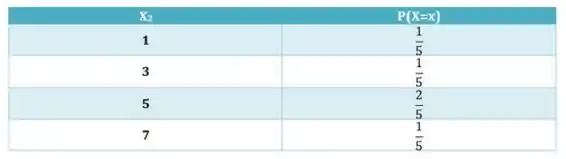
Passo 4
Montando a tabela de distribuição de e
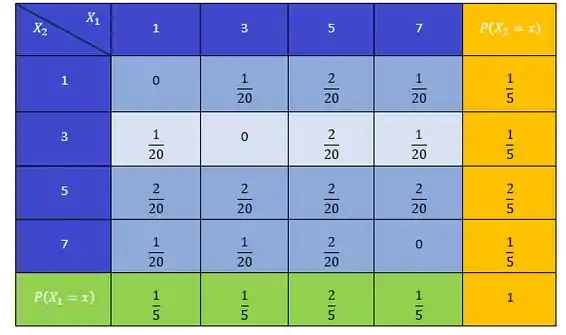
Só tá faltando uma coisa, elas são independentes?
Se nós olharmos para tabela de cima, veremos que e NÃO são independentes, pois os produtos marginais NÃO são iguais as caselas.
Passo 5
Por fim, vamos encontrar a média e a variância de , e .
Notem, que COM ou SEM reposição e são as mesmas, logo
Como e não são independentes, da distribuição conjuta temos:
A partir dessa tabela, temos
Resposta
Letra (a)
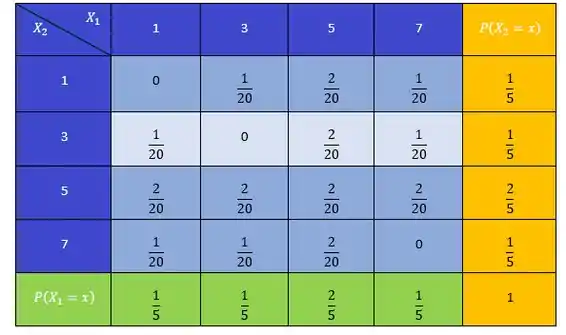
Letra (b)
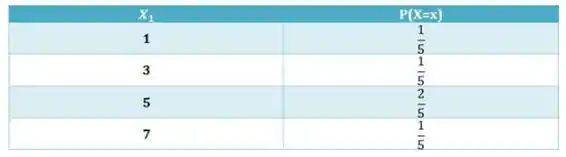
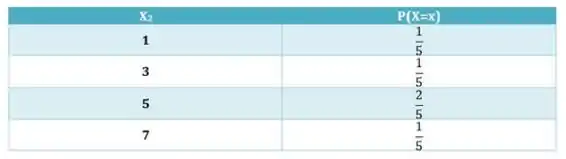
Não são independentes, pois os produtos das marginais não são iguais as caselas.
Letra (c)