Enunciado

Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 4.Problemas - Ex. 27

Usando os dados da Tabela 2.1, Capítulo 2:

(a) Construa a tabela de distribuições de freqüências conjunta para as variáveis salário e idade, mas divida cada uma delas num certo número de intervalos de classe.

(b) Como poderia ser calculado o coeficiente de correlação baseado nessa tabela?

(c) Você conseguiria “escrever” a fórmula da correlação para dados agrupados?

Passo 1

(a) Construa a tabela de distribuições de freqüências conjunta para as variáveis salário e idade, mas divida cada uma delas num certo número de intervalos de classe.

Primeiro, precisamos dos dados da Tabela 2.1, né? Especificamente os dados das variáveis salário e idade.

Essa tabela se encontra na página 11, beleza? 😉

Vamos lá!

Já construímos diversas tabelas de distribuições de frequências conjuntas, a única coisa que muda agora, é que a letra (a) pede para que a gente divida as variáveis em um certo intervalos de classe.

Mas para que dividir e como construir esses “intervalos de classes”?

Algumas vezes, para evitar um grande número de entradas, agrupamos os dados marginais em intervalos de classes, de modo semelhante ao resumo feito no caso unidimensional.

Podemos dividir em n intervalos e de diversas formas diferentes, certo?

Construindo uma possível tabela, temos

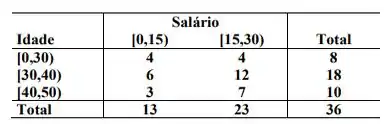
Passo 2

(b) Como poderia ser calculado o coeficiente de correlação baseado nessa tabela?

Quando a gente constrói uma tabela de frequências com intervalos de classe e temos que calcular a média, por exemplo. O que nós fazíamos?

Utilizamos os pontos médios de cada categoria, né?

Advinha como poderia ser calculado o coeficiente de correlação?

Só termos o mesmo racíciocio, logo o cálculo do coeficiente de correlação neste caso, poderia ser feito utilizando-se os pontos médios de cada categoria.

Passo 3

Já vimos o bizu na letra (b), né? Ele vai nos ajudar bastante, mas precisamos sacar mais uma coisinha.

Vamos olhar para o nosso elemento da 1° linha com a 1° coluna.

4!!! Ou seja, 4 indivíduos têm idade entre [0,30) e recebem entre [0,15). Ponto médio da idade: 15, e ponto médio do salário: 7,5. Logo como são 4 indivíduos, temos 4 pares (15; 7,5) repetidos, certo?

Se nós fizermos isso para todos os dados do interior da tabela, temos que o cálculo do coeficiente de correlação agrupados poderia ser feito com a fórmula usual, onde haveria 4 pares (15;7,5) repetidos, 6 pares (35;7,5) repetidos, etc. Assim, a fórmula seria:

onde , são os pontos médios,

Resposta

(a)

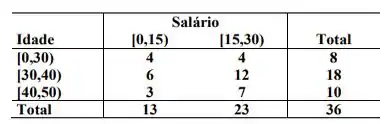
(b) O cálculo do coeficiente de correlação neste caso, poderia ser feito utilizando-se os pontos médios de cada categoria.

(c) Com a idéia que foi descrita no item anterior, o cálculo do coeficiente de correlação agrupados poderia ser feito com a fórmula usual, onde haveria 4 pares (15;7,5) repetidos, 6 pares (35;7,5) repetidos, etc. Assim a fórmula seria:

onde , são os pontos médios,

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para verificar a homogeneidade das duas populações do problema anterior, um estatístico sugeriu que se usasse o quociente F = v a r ( X / A ) v a r ( X / B ) , mas não disse qual decisão tomar baseado

Para se estudar o desempenho de duas corretoras de ações, selecionou-se de cada uma delas amostras aleatórias das ações negociadas. Para cada ação selecionada, computou-se a porcentagem de lucro apres

Como vimos na seção 3.3 , o desvio padrão é bastante afetado pela magnitude dos dados, ou seja, ele não é uma medida resistente. Se quisermos comparar a variabilidade de dois conjuntos de dados podemo

Use os resultados dos exercícios 1.28 e 1.29 para criar um gráfico que ilustre a evidente interação dos dados. Use o gráfico da Figura 1.3 no Exemplo 1.3 como guia. O tipo de informação contido nos ex

Considere a situação do Exercício 1.28, mas agora use o seguinte conjunto de dados, no qual o encolhimento é medido novamente em velocidades de injeção baixa e alta. Entretanto, dessa vez a temperatur