Enunciado
Probabilidade e Estatística - Magalhães e Lima - Noções de Probabilidade de Estatística - Ed: 6º - Capítulo 5.2 - Ex. 6b
A variável é Bernoulli com e é Binomial com . Admita que são independentes.
- Determine
- Obtenha a função de probabilidade conjunta do X e Y e do produto XY.
- Calcule e verifique que: .
- Determine o valor de e de
Passo 1
- X pode assumir os valores {0, 1}, Y pode assumir os valores {0, 1, 2, 3}, vamos usar nosso conhecimento dos modelos discretos para calcular as marginais e facilitar nossa vida:
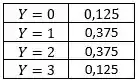
Passo 2
Para montar a conjunta vamos multiplicar os valores das marginais, de acordo com o par da conjunta que estivermos lidando:
Passo 3
Para calcular temos que multiplicar os valores dos pares verificar o valor deles, e somar todas as probabilidades que tiverem o mesmo valor, por exemplo, a probabilidade conjunta dos pares devem ser somadas já que o produto deles é sempre 0:
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Sorteiam-se bolas de uma urna que contém inicialmente 20 bolas vermelhas e 10 bolas azuis.(a) Qual é a probabilidade de que todas as bolas vermelhas sejam retiradas antes de todas as azuis?Agora supon
Uma urna contém inicialmente 1 bola vermelha e 1 bola azul. Em cada rodada, uma bola é retirada aleatoriamente e substituída por duas outra bolas de mesma cor (por exemplo, se a bola vermelha ê a prim
Duas fábricas locais, A e B , produzem rádios. Cada rádio produzido pela fábrica A tem probabilidade de 0,05 de apresentar defeitos, enquanto cada rádio produzido pela fábrica B tem probabilidade de 0
Suponha que 5 % dos homens e 0,25 % das mulheres sejam daltônicos. Uma pessoa daltônica é escolhida aleatoriamente. Qual é a probabilidade dessa pessoa ser um homem? Suponha que exista um mesmo número
No Exemplo 3 f , suponha que a nova evidência esteja sujeita a possíveis interpretaçōes e de fato mostre que é apenas 90 % provável que o criminoso possua a característica em questão. Neste caso, qual