Operações de Vetores e Matrizes
Produzido por Gustavo BarbosaTeoria
Opa e ae, tudo em cima?
A conversa de hoje vai ser beeem mais prática, ok? Então já vai abrindo aí o Matlab para irmos fazendo as coisas juntos.
A forma de realizar operações com vetores e matrizes muda muito de acordo com a linguagem de programação que tá sendo usada e geralmente, essas não são tarefas muito fáceis.
Maaas como o Matlab foi construído para trabalhar com matrizes, essas operações aqui são bem mais simples e é isso que vou te ensinar hoje!
Além disso, como na grande maioria dos casos o Matlab não diferencia vetores e matrizes, tudo que vamos ver vale pra ambos.
Belezinha?

Mas que operações são essas que vamos realizar?
Bora descobrir!
Operações aritméticas
Bem galera, aqui vamos dividir em dois grupos: as operações de soma e subtração e as operações de multiplicação.
- Soma e subtração
- Multiplicação
Um vetor ou uma matriz se somam da mesma forma que uma variável comum, similar ao que estávamos fazendo até o presente momento. Então:
Então isso vale se e forem variáveis simples, vetores ou matrizes!
Porém, quando se trabalha com vetores e matrizes, existe uma restrição: ambas as variáveis precisam ter as mesmas dimensões.
Caso você esteja se perguntando... “ Mas o que é isso? ”

Calminha, vamos simplificar isso! Se você tem uma matriz de 2 linhas e 2 colunas, você não poderá somar ou subtrair essa matriz de uma outra matriz de 3 linhas e 3 colunas.
Vamos para o exemplo:
Imagine que temos uma matriz M e outra B. Vamos escrever elas no Matlab e tentar somar as mesmas, ok?

Logo vimos que não é possível somar, pois o Matlab acusa erro.
No caso da multiplicação, também temos uma limitação que vem da matemática: o número de colunas da primeira matriz tem que ser igual ao número de linhas da segunda.
Se quisermos multiplicar uma matriz com 2 linhas e 2 colunas por um vetor, ele obrigatoriamente precisa ser do tipo coluna com dois elementos.
Agora que sabemos dessa restrição vamos ver como multiplicar para resolver alguns exemplos.
No caso de trabalhar com vetores e matrizes, o Matlab tem duas formas de multiplicar: a primeira é a forma usual da multiplicação de matrizes que aprendemos na matemática e na segunda forma ele multiplica elemento a elemento da matriz.
A sintaxe das operações aritméticas são:
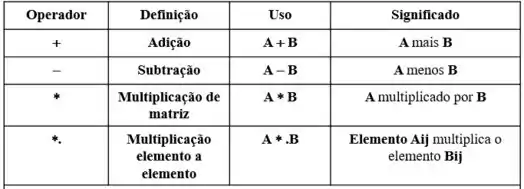
Por exemplo vamos multiplicar a matriz M por ela mesma das duas formas:
A primeira forma é a multiplicação convencional de matriz onde a sintaxe é dada por

Já a segunda forma é a multiplicação elemento a elemento onde a sintaxe é dada por :

Em outro exemplo, vamos multiplicar a matriz por um vetor

Um extra: esse ponto não serve apenas para a multiplicação, se eu quiser elevar cada elemento da matriz a alguma potência, por exemplo a quadrado basta colocar .
Então, de forma geral, esse ponto antes da operação indica “cada elemento”, ou seja, se traduz em pegue cada elemento de M e eleve ao quadrado.
Funções Vetoriais
Aqui vamos tratar das funções vetoriais, as funções vetoriais na realidade são as mesmas funções que vimos nos tópicos de funções, só que lá elas operavam em uma variável escalar, ou seja um valor. Aqui elas operam no conjunto de valores em um vetor.
Vamos lá fazer uns exemplos:
Imagine que você tem um vetor do tipo e deseja calcular o seno desse vetor. Inserindo o vetor no Matlab, temos:

Outro exemplo que podemos ver é caso da divergência de um vetor. Pra isso, vamos criar um vetor simbólico, ok?
A função divergência é calculada da forma :
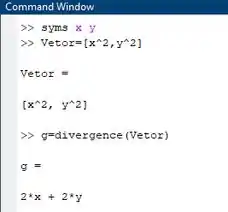
Logo, todas as funções matemáticas que usamos nas variáveis escalares funcionam com vetores!
Algumas funções vetoriais
Agora vamos conversar sobre algumas funções do Matlab que auxiliam no trabalho de vetores e matrizes, e essas funções estão tabeladas logo abaixo:

Por exemplo, vamos calcular o determinante de uma matriz utilizando a tabelinha. Primeiramente inserimos a matriz :
Se você digitou tudo certinho vai aparecer algo assim:

Beeem pessoal eu sei que a conversa ficou grande e então iremos ficar por aqui, lembre-se, não deixe de praticar pois quando se trata de programação quanto mais treinar melhor fica.
Iae essa aula te ajudou? Responde Ai.
Operações aritméticas
Funções Vetoriais
Algumas funções vetoriais
Exercícios Resolvidos
Exercício Resolvido #1
UTFPR – EL71E – Algoritmos – P1
Leia os vetores abaixo e escreva um programa que calcule a média e a soma dos mesmos.a
- u=(1, 2, 3, 4) e v=(5, 6, 7, 8)
- u é um vetor que varia de 0 até 10 variando de um em um, e um vetor v que varia de 20 até 30 variando de em um.
Passo 1
Para começar precisamos inserir os vetores no Matlab.
Primeiramente inserimos o u e v.
U=[1 2 3 4]
V=[5,6,7,8]
Agora iremos calcular a soma e a média dos vetores, para a soma temos:
K=U+V
E para calcular a média precisamos da função:
D=mean(K)

Passo 2
Para começar precisamos inserir os vetores no Matlab.
Primeiramente, inserimos o u e v.
U=0:1:10
V=20:1:30
Agora iremos calcular a soma e a média dos vetores, para a soma temos:
K=U+V
E para calcular a média precisamos da função:
D=mean(K)

Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
“Elaboração Própria”
Calcule as seguintes expressões abaixo:
- Calcule a divergência de z
- A matriz A é dada por e calcule a matriz inversa de
- Dado o vetor calcule o cosseno desse vetor.
Passo 1
Para calcular a divergência do vetor, precisamos primeiramente inseri-lo de forma simbólica.
Isso torna-se necessário porque estamos com variáveis que não tem um valor numérico definido, então a única forma de calcular essas operações no Matlab é via variável simbólica. Operações realizadas em função de algo que não apresente um valor numérico exige que indiquemos no Matlab que as variáveis são simbólicas.
Pensa comigo, se eu não digo quais são as variáveis de entrada, qual é a entrada de dados? Ou seja, o primeiro bloco da programação é nulo, vou realizar uma operação em algo que eu não defini, por isso utiliza-se variável simbólica nessa alternativa.
E relembrando uma coisa que já foi vista em outros tópicos: quando se define uma variável simbólica, isso está além de se a natureza é vetorial ou escalar, ou seja, a variável simbólica serve tanto para funções escalares quanto para funções vetoriais.
Após isso utiliza a função divergência para calcular o divergente do vetor.

Aqui o Matlab separou os elementos do vetor Z por uma vírgula, isso é algum elemento da sua própria configuração que porventura desconheço o motivo, pois podemos separar os elementos de uma linha de duas formas a primeira é o que utilizamos que é espaçamento simples a outra é colocar uma vírgula.
Por algum motivo meu Matlab está configurando assim, mas tanto um quanto o outro está correto.
Mas o que importa é que na workspace ele está entendendo que estou criando um vetor linha como mostrado abaixo:

Passo 2
Para resolver essa questão primeiramente precisamos inserir a matriz e após isso utilizamos a função inversa vista na tabela da aula, logo precisamos implementar a matriz dentro do Matlab.
Primeiramente vamos inserir a primeira linha onde precisamos espaçar os elementos apenas com um espaçamento simples.
A
Para implementar a segunda linha precisamos dar um “;” para indicar que vamos implementar a segunda linha e vamos separar cada elemento da segunda linha por um espaçamento simples, resultando a seguinte matriz:
A
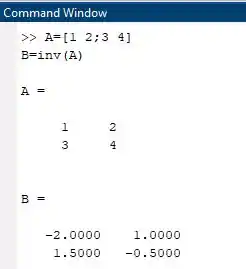
Passo 3
E ae galera vamos resolver esse problema? Para isso primeiramente vamos inserir k vetor ok?
Uma vez que o vetor está inserido, vamos apenas calcular o cosseno desse vetor, ou seja, vamos calcular o cosseno de cada elemento dentro do vetor.
Para isso precisamos apenas chamar a função cosseno e no seu argumento de entrada inserir o vetor que desejamos calcular o cosseno.
Sendo assim, a sintaxe se torna:
Onde a variável Y está nos mostrando o cosseno de cada elemento do vetor V.

Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3
“Elaboração Própria”
Em uma rotina, crie as seguintes matrizes:

Na mesma rotina:
- Calcule A + B e B + A para mostrar que a adição de matrizes é comutativa.
- Calcule A + (B + C) e (A + B) + C para mostrar que a adição de matrizes é associativa.
- Calcule 5(A + C) e 5A + 5C para mostrar que, quando matrizes são multiplicadas por um escalar, a multiplicação obedece a distributividade em relação à soma
Passo 1
Para resolver qualquer alternativa dessa questão precisamos inserir esses três matizes primeiramente, logo
A=[5 2 4 ; 1 7 -3 ; 6 -10 0]
B=[11 5 -3; 0 -12 4 ; 2 6 1]
C=[7 14 1;10 3 -2; 8 -5 9]
Para calcular as alternativas precisamos inserir apenas as expressões de cada Alternativa

- Agora precisamos somar
- Agora calcular as expressões
- Basta inserir as expressões da letra C
W=A+B
W=B+A

W=A + (B + C)
W=(A + B) + C

W=5*(A + C)
W=5*A + 5*C
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #4
Elaboração Própria
Considere a função . Crie uma rotina que determine o valor de y para os seguintes valores de
Dica: Gere inicialmente, dentro da rotina, o vetor x. Em seguida, resolva o problema para o vetor y, usando operações elemento a elemento.
Passo 1
Inicialmente iremos criar o vetor, se você analisar bem veremos que existe um padrão na progressão desse vetor, pois ele começa em e a cada elemento ele soma
Então para criar o vetor podemos utilizar o segundo método mais prático ao invés de ficar inserindo elemento a elemento, logo.
Agora para criar essa operação elemento a elemento precisamos lembrar que para fazer a multiplicação elemento a elemento e elevar a uma certa potência antes da operação precisa colocar o pontinho como vimos na tabela aritmética, sendo assim a função fica
Se escreveu tudo certinho no Matlab temos:

Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #5
Elaboração Própria
Crie uma rotina para resolver o seguinte sistema de equações lineares com o Matlab:
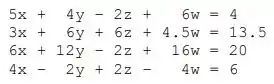
Dica : deixe o sistema na forma matricial e utilize a última tabela da aula de matrizes e operações
Passo 1
Primeiramente para resolver essa questão precisa reescrever o sistema de equações sob a forma matricial, sendo assim esse sistema na forma matricial se torna:
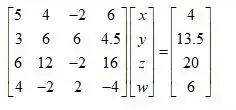
E vamos chamar a matriz de coeficientes de A e o vetor à direita da equação de b.

Para resolver esse sistema de equações lineares basta lembrar da função linsolve que está na tabelinha da aula.
Agora vamos programar!
Passo 2
O código no Matlab se torna algo mais ou menos assim. Primeiro vamos declarar 4 vetores e cada um deles corresponde a uma das linhas da matriz A. Para formar vetores, os elementos são separados por espaços.
V1 = [5 4 -2 6]
V2 = [3 6 6 4.5]
V3 = [6 12 -2 6]
V4 = [4 -2 2 -4]
Agora que temos suas linhas definidas, criamos a matriz A com os elementos (as linhas) listadas na ordem correta e separadas por ponto e vírgula.
A = [ V1 ; V2 ; V3 ; V4 ]
O vetor b é uma matriz coluna, então também terá seus elementos separados por ponto e vírgula.
B = [ 4 ; 13.5 ; 20 ; 6 ]
Agora usamos o comando linsolve pra resolver o sistema de equações. Nos argumentos entram a matriz de coeficientes A e o vetor de termos independentes b, nessa ordem.
X = linsolve (A,b)
Passo 3

Agora o Matlab irá montar a matriz e resolver com a função:

Resultando X=0,9433 y=1,8821 z=0,7415 w=-1,1270
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #6
Elaboração Própria
Dado o sistema de equações:
Encontre os valores de pertencente aos reais, pelo o qual o sistema de equações possui uma solução única e real.
Passo 1
A questão é uma aplicação de resolução de sistema de equações lineares, tem diversas formas de fazer ela.
Porém, dessa vez iremos resolver pelo método da matriz inversa. Pois, como geralmente é mostrado no ensino médio seja um sistema de equações na forma matricial.
Se pudermos escrever o sistema da seguinte forma:
Nós temos que a solução é
Então, para resolver essa questão precisamos explicitar todas as soluções em função de
E assim julgar os valores de pelo o qual nosso sistema satisfaz as condições desejadas da questão.
Passo 2
Analisando o sistema de equação podemos notar que podemos decompor em três matrizes, que são as matrizes:
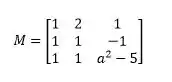
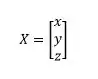

E podemos perceber que se realizarmos a seguinte operação matricial:
Iremos retornar para o sistema de equações originais.
Logo, para resolver o sistema de equações precisamos implementar primeiramente essas três matrizes no Matlab.
Então vamos lá.
Passo 3
Primeiramente precisamos notar que quando formos inserir essa matriz no Matlab existe uma variável simbólica dentro, isso mesmo é a variável .
Então vamos primeiramente defini-la como uma variável simbólica.
Agora vamos inserir as matrizes, se caso você inserir cada matriz certinho deve chegar em algo mais ou menos assim:

Uma vez que implementamos precisamos resolver o sistema de equação linear, para isso vamos usar a função inversa.
Basta escrever na sua Workspace a seguinte equação:
Ou seja, a solução é a inversa da matriz M multiplicado pela matriz B e chegaremos no seguinte conjunto de soluções:

Passo 4
Para finalizar vamos analisar as soluções, como podemos ver todas as soluções têm denominadores do tipo , onde as raízes são .
Ou seja, quando o valor de é igual a o denominador da , e como sabemos da matemática básica qualquer divisão por zero é uma indeterminação.
Ou seja, excerto qualquer outro valor de produz uma solução única e real.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #7
Elaboração Própria
Dada a matriz:
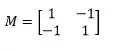
A operação é igual a:
Passo 1
Essa questão é uma questão bem típica da álgebra linear que existe uma demanda de cálculos consideravelmente grande.
Para a resolução analítica da questão devemos lembrar das operações de multiplicação de matrizes, que equivale por exemplo a:
Agora imagina só, você realiza essas operações até resolver aqueles polinômios da questão?
Trabalhoso demais né?
Ai que vem a vantagem de resolver isso no Matlab, iremos precisar apenas de duas linhas.
A primeira vamos inserir a matriz e na segunda linha vamos inserir o polinômio, pois, quando eu indico no Matlab a operação ele automaticamente já entende que tou fazendo
E isso funciona com as demais potências.
Passo 2
Agora que já discutimos a questão no passo 1, vamos inserir a matriz dentro do Matlab.
Para isso vamos precisar lembrar da sintaxe, para inserirmos os elementos da primeira linha precisamos apenas separar os elementos por espaços simples dentro de uma chave.
Logo a primeira linha da matriz fica:
Agora precisamos inserir a segunda linha basta colocar o ponto e vírgula, isso indica ao Matlab que vamos começar a escrever a segunda linha da matriz, logo:
Uma vez que inserirmos a matriz no Matlab, vamos agora implementar o polinômio da questão em si da seguinte forma:
Passo 3
Inserindo tudo na janela de command Windows deve mostrar algo mais ou menos assim para você:
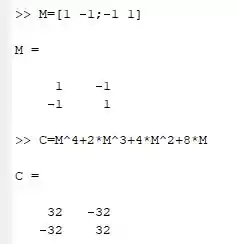
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #8
Elaboração Própria
Dada as seguintes matrizes:
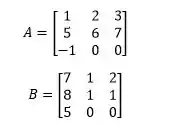
E uma suposta Matriz C que é dada pelo produto das Matrizes A e B, qual é o elemento da matriz C?
Passo 1
Opa galerinha, essa questão é uma questão bem típica de exercícios de geometria analítica.
A ideia aqui é executar a multiplicação entre as matrizes para poder identificar o elemento da matriz .
Não é uma tarefa muito difícil de fazer manualmente, porém, o Matlab está aí para facilitar nossas vidas, então vamos lá utilizá-lo.
Primeiramente precisamos implementar cada matriz no Matlab, após isso basta realizar o produto das matrizes A e B e rapidamente teremos a matriz C.
Mas como identificar o elemento ?
Basta usar o comando
Esse comando faz o seguinte, ele procura o elemento da intersecção entre a segunda linha e segunda coluna da Matriz C e o anexa na variável G que você mesmo definiu, respondendo assim a sua questão.
Passo 2
Agora que já discutimos a questão no passo 1, vamos inserir a matriz dentro do Matlab.
Para isso vamos precisar lembrar da sintaxe, para inserirmos os elementos da primeira linha precisamos apenas separar os elementos por espaços simples dentro de uma chave.
Logo a primeira linha da matriz fica:
Agora precisamos inserir a segunda linha basta colocar o ponto e vírgula, isso indica ao Matlab que vamos começar a escrever a segunda linha da matriz, logo:
Seguindo essa regrinha sucessivamente podemos escrever as Matrizes e da seguinte forma:
E consequentemente a Matriz C é dada por
E para descobrir o Elemento da matriz C que nos interessa basta escrevermos:
Que isso irá procurar na matriz C o elemento e anexá-lo na variável C imprimindo na janela de command windows
Passo 3
Inserindo tudo na janela de command Windows deve mostrar algo mais ou menos assim para você:

Resposta
Ei, a resposta está no passo a passo :)