Algumas funções úteis – Parte 2
Produzido por Gustavo BarbosaTeoria
Introdução
Fala, galera! O MATLAB é uma ferramenta tão poderosa, com tantas funções úteis para mexer com matrizes e vetores, que tivemos que fazer uma segunda parte para apresentar mais algumas funçõezinhas que facilitam muito nossa vida.
Hoje, vamos ver algumas funções com vetores e matrizes que são muito úteis nas engenharias. Capaz de, depois dessa aula, quando você vir uma matriz, só querer usar o MATLAB. Bora lá?

Autovalores e Autovetores
Em álgebra linear, aprendemos a calcular os autovalores e os autovetores de uma matriz. Quando é uma matriz , temos que resolver uma equação do grau para encontrar os autovalores e os autovetores. Com uma matriz , a coisa complica um pouco, mas vá lá, com jeitinho dá pra resolver na mão.
Mas e se for uma matriz beeeem grande, tipo uma ? Tem que ferver os miolos para chegar numa solução, até ter um ataque de raiva e desistir de tudo?

Não se desespere, jovem gafanhoto, o MATLAB taí para resolver para você! Com apenas uma linha de código, você consegue encontrar os autovalores e os autovetores de uma matriz, com a função . Para ver como ela funciona, vamos usar como exemplo a matriz A abaixo:
No MATLAB, entramos com as seguintes linhas de código:
Na primeira linha, entramos com a matriz e aplicamos a função na matriz que criamos, na segunda linha.
A função nos retorna as matrizes e . As colunas da matriz são os autovetores e a matriz é uma matriz diagonal com os autovalores. O print com o código no MATLAB ajuda a entender:

A partir das colunas da matriz , vemos que os autovetores da matriz são e . A partir dos elementos da diagonal principal da matriz , temos que os autovalores de são e . Bem prático, não?

Funções Estatísticas
Bora pras próximas funções! Imagine que você realizou um experimento para medir a densidade de alguns materiais e precisa fazer a análise estatística dos resultados, registrados na tabela abaixo:

Você quer determinar qual é a densidade média, o desvio padrão, o material mais denso e o menos denso. Você pode usar o MATLAB pra isso, e ele pode até mesmo te indicar em qual posição da lista o material de densidade máxima ou mínima se encontra.
A primeira coisa que temos que fazer é entrar com um vetor com valores das densidades, que vou chamar de , na mesma ordem da tabela:
Primeiro, vamos calcular a média aritmética e o desvio padrão das densidades de nossos materiais. Para a média, usamos a função :
E para o desvio padrão, usamos a função :
A sintaxe das duas funções é bem parecida: na esquerda escrevemos a variável que vai guardar o resultado que queremos calcular, então colocamos o sinal de igual, escrevemos a função que vamos usar e por fim entre parênteses, o conjunto de dados onde a função será aplicada.
No MATLAB, temos os seguintes resultados:

Então, a densidade média de nossos materiais é de e foi armazenada na variável. Já o desvio padrão é de e foi armazenado na variável .
Para encontrar o valor mínimo e sua posição no vetor, podemos usar a função , pedindo que ela nos dê essas informações, usando a seguinte linha de código:
A linha de código acima quer dizer que a função vai me dar a densidade mínima, armazenada na variável , e vai me dar a posição dela no vetor , armazenada na variável . Bora ver como isso fica no MATLAB?

Podemos ver que a densidade mínima é , correspondendo à madeira na nossa tabela, e que ela é o sexto elemento do vetor .
Podemos encontrar a densidade máxima da nossa tabela usando a função . Ela funciona igualzinho à função , só que retorna o maior valor. Entrando a seguinte linha de código no MATLAB:
Ele nos dá o seguinte resultado:

A densidade máxima é e esse valor foi armazenado na variável . Vemos também que ela é o nono elemento do vetor , correspondendo à platina na nossa tabela.
Um detalhezinho importante sobre as funções e : caso você não precise descobrir a posição do valor máximo/mínimo, você pode eliminar da sua linha de código a variável que armazena a posição. No exemplo da densidade, caso eu quisesse só encontrar o maior valor do vetor , sem me importar com a posição, eu alteraria o código para:
O MATLAB me retornaria o mesmo valor de , mas não me daria a posição dele no vetor.
Encontrar os valores mínimo e máximo de uma lista e as suas posições na lista parece ser bem fácil com uma lista pequena como a da nossa tabelinha. Mas imagina ter que fazer isso com uma lista de elementos? Ainda bem que o MATLAB faz isso para a gente ;D
Uma dica antes de encerrar essa aula: você pode encontrar mais informações sobre as funções que explicamos aqui e muitas outras no site oficial da MathWorks, a criadora do MATLAB, basta procurar “matlab” e o nome da função no buscador. Geralmente é o primeiro link que aparece. Lá tem exemplos e outras formas de usar as funções que podem ser úteis dependendo do que você quiser fazer.
E aí? Curtiu conhecer essas funçõezinhas? Agora é praticar, segue lá para os exercícios ;D
Funções Estatísticas
Exercícios Resolvidos
Exercício Resolvido #1
“Autoria própria”
Na definição de autovalores e autovetores, temos que, dada uma matriz quadrada A:
onde V é uma matriz cujas colunas correspondem aos autovetores e D é uma matriz diagonal, em que os elementos da diagonal principal são os autovalores da matriz A.
Usando o MATLAB, dada a matriz:
- Encontre os autovalores e os autovetores de A;
- Verifique a igualdade .
Passo 1
A questão pede que apliquemos diretamente a função eig() do MATLAB na matriz A (letra a da questão) e, em seguida, verifiquemos a igualdade (letra b). Usando diretamente as saídas da função eig(), podemos resolver a letra b, já que a função eig()nos retorna as matrizes V e D exatamente no formato descrito no enunciado.
Passo 2
Vamos começar com a letra a, que nos pede para encontrar os autovalores e os autovetores da matriz A. Primeiramente, temos que entrar com a matriz A no MATLAB, no Command Window, com a seguinte linha de código:
A = [6 7 1 8; 5 3 1 7; 3 6 5 7; 0 7 4 0]
No Command Window do MATLAB, fica assim:

Em seguida, aplicamos diretamente a função eig() para encontrar os autovalores e os autovetores de A, entrando com o seguinte comando do Command Window:
[V,D] = eig(A)
Com esse comando, pedimos à função eig() que nos informe os autovalores e os autovetores de A e ela nos retorna duas matrizes: V e D. vamos ver como isso fica no MATLAB:
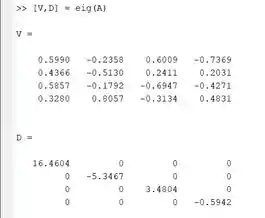
A matriz V apresenta os autovetores de A: cada coluna de V é um autovetor de A. Já a matriz D é uma matriz diagonal que nos apresenta os autovalores de A. Cada elemento da diagonal principal de D é um autovalor.
Portanto, os autovetores da matriz A são:
E os autovalores são:
Passo 3
Concluindo a letra a da questão, temos as matrizes V e D para verificar a igualdade . Primeiramente, fazemos o produto e em seguida, o produto , e comparamos os resultados. Vamos ver como fica no Command Window do MATLAB:
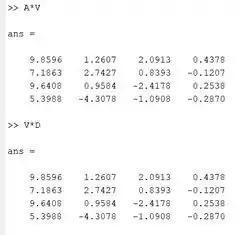
Veja que os resultados são idênticos. Logo, .
Resposta
- Os autovetores da matriz A são:
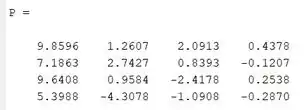
- Utilizando [V,D] = eig(A) , encontramos as matrizes V e D no formato adequado para verificar a igualdade . O produto e o produto resultam na mesma matriz, que chamarei de P, apresentada abaixo:
E os autovalores são:
Exercício Resolvido #2
“Autoria própria”
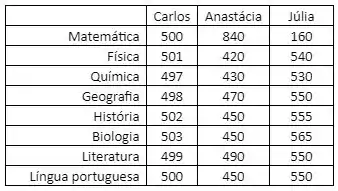
Três amigos prestaram um vestibular e as notas que eles tiraram em cada disciplina são apresentadas na tabela abaixo:
Usando o MATLAB, responda as seguintes perguntas:
- Qual dos três teve a maior nota média?
- Qual dos três apresentou menor variação de desempenho em relação à média de notas nas disciplinas?
Passo 1
Na letra a, a questão nos pede para calcular a média das notas de três amigos que prestaram vestibular. Neste caso, temos que entrar com as notas de cada pessoa, em forma de vetor, e aplicar diretamente a função mean() do MATLAB.
A letra b nos pede para determinar qual pessoa apresentou menor variação de desempenho em relação à média nas disciplinas. Isso pode ser verificado usando o desvio padrão das notas, que é um parâmetro que indica o grau de variação. Quanto maior for o desvio padrão, maior é a variação em relação à média. Logo, precisamos ver qual dos três amigos tem o menor desvio padrão. Para isso, usamos a função std() do MATLAB e comparamos os resultados dos três amigos.
Passo 2
Primeiramente, vamos entrar com as notas do Carlos, da Anastácia e da Júlia no MATLAB. As notas de cada um serão entradas em forma de vetor, usando as seguintes linhas de código no Command Window:
carlos = [500 501 497 498 502 503 499 500]
anastacia = [840 420 430 470 450 450 490 450]
julia = [160 540 530 550 555 565 550 550]
No MATLAB, ficou assim:

Indiquei o vetor de notas de cada um pelo nome da pessoa, mas você pode chamar como quiser.
Agora, vamos calcular a média das notas usando a função mean(). Entre no Command Window as seguintes linhas de código:
media_c = mean(carlos)
media_a = mean(anastacia)
media_j = mean(julia)
Nessas linhas de código, a média das notas de cada um é armazenada em uma variável chamada media_c, media_a e media_j, com a inicial do nome de cada um. Novamente, você pode chamar essas variáveis como quiser. Vamos ver como ficou no MATLAB, com ele já nos apresentando o resultado:
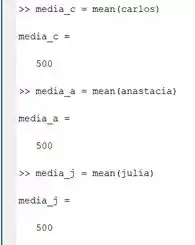
No final das contas, os três apresentaram a mesma média de notas, 500.
Passo 3
Agora vamos resolver a letra b da questão. Ela nos pergunta qual dos três amigos teve a menor variação de desempenho. Para descobrirmos isso, precisamos calcular o desvio padrão das notas de cada um, usando a função std(). Entramos no MATLAB as linhas de código:
d_pad_c = std(carlos)
d_pad_a = std(anastacia)
d_pad_j = std(julia)
Nas linhas de código, o desvio padrão das notas é armazenado em uma variável chamada d_pad_c, d_pad_a e d_pad_j, com a inicial do nome da pessoa. O print do Command Window nos apresenta os resultados:
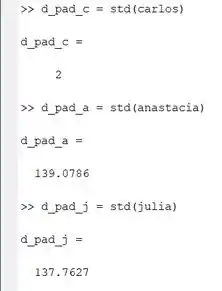
Dos três amigos, Carlos foi quem teve a menor variação de desempenho, pois o desvio padrão de suas, d_pad_c, é o menor.
Resposta
- Carlos, Anastácia e Júlia tiveram a mesma nota média: 500.
- Carlos foi quem apresentou a menor variação de desempenho em relação à nota média, pois o desvio padrão de suas notas é o menor.
Exercício Resolvido #3
“Autoria própria”
A tabela abaixo apresenta os dados de uma curva de torque de um motor à combustão.

Com o MATLAB, encontre o torque máximo e determine a velocidade em que o motor atinge o torque máximo.
Passo 1
A curva de torque de um motor à combustão e uma curva de torque em função da velocidade de rotação do motor. A questão nos pede para encontar o torque máximo de um motor a partir dos dados da curva torque, e a velocidade angular do motor que faz com que ele atinja esse torque máximo.
Para resolvermos a questão, usaremos a função max() do MATLAB, pedindo que ela nos retorne o torque máximo de um vetor de torques e que ela nos indique a posição do torque máximo no vetor. Em seguida, usaremos essa posição para achar a velocidade do motor correspondente ao torque máximo.
Passo 2
Primeiramente, vamos criar dois vetores no MATLAB: um contendo a rotação do motor, isto é, os valores da primeira coluna da tabela do enunciado, e outro contendo o torque do motor, com os valores da segunda coluna da tabela. Para isso, entre com os dois vetores abaixo no Command Window:
vel = [0 500 750 968.75 1187.5 1406.25 1625 1843.75 2062.5 2281.25 2500]
torque = [100 500 750 1344 1588 1641 1654 1635 1560 1464 1365]
O vetor vel contém os valores da primeira coluna da tabela, na mesma ordem, correspondendo a velocidade de rotação do motor. O vetor torque contém os valores da segunda coluna da tabela, na mesma ordem, correspondendo ao torque do motor. Vamos ver como ficou no MATLAB?

Passo 3
Depois de entrarmos com os vetores vel e torque, usamos a função max() para encontrar o torque máximo. Entre no Command Window o comando:
[max_torque,indice] = max(torque)
Nesse comando, pedimos ao MATLAB que ele nos informe o elemento de máximo valor dentre os elementos do vetor torque. O valor máximo é armazenado na variável max_torque.
Pedimos também ao MATLAB que nos informe a posição do valor máximo no vetor. A posição é armazenada na variável indice. Vamos ver o que deu?

Descobrimos que o torque máximo é de 1654 Nm e está na posição 7 do vetor torque. Podemos verificar lá na tabela do enunciado e vemos que é isso mesmo: o torque máximo da tabela é 1654 Nm e ele está na oitava linha da tabela, que corresponde à sétima posição na lista de valores, se desconsiderarmos a primeira linha, que contém o cabeçalho com a informação “Torque [Nm]”.
Passo 4
Sabendo a posição do torque máximo no vetor torque, podemos encontrar a velocidade correspondente, pois os vetores torque e vel contêm os valores da tabela do enunciado, na mesma ordem em que são listados na tabela. Para isso, usamos o seguinte comando:
vel_max = vel(indice)
Com esse comando, eu peço ao MATLAB que me informe o valor do vetor vel que está na posição indice e o armazene na variável vel_max.
Como vimos no passo anterior, a variável indice é igual a 7, logo o MATLAB vai me dar a velocidade que está na posição 7 do vetor vel, resultando em:

Podemos verificar na tabela: a velocidade à esquerda do torque máximo de 1654 Nm é 1625 rpm. O valor de 1625 rpm está na oitava linha da tabela, correspondendo à sétima posição na lista de velocidade de rotação, desconsiderando o cabeçalho.
Resposta
O torque máximo do motor é 1654 Nm e é atingido quando o motor tem uma rotação de 1625 rpm.
Exercício Resolvido #4
Exercício adaptado de: “Probabilidade & Estatística para Engenharias e Ciências” (8ª edição), escrito por Ronald E. Walpole, Raymond H. Myers, Sharon L. Myers e Keying Ye.
Acredita-se que a resistência à tensão da borracha siliconizada seja uma função da temperatura de cura. Um estudo foi realizado, no qual amostras de 12 espécimes de borracha foram preparadas usando temperaturas de cura de 20 °C e 45 °C. A tabela abaixo mostra os valores de resistência à tensão, em megapascals, para cada temperatura:
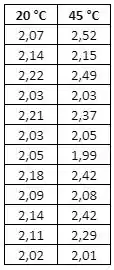
Usando o MATLAB, responda às seguintes questões:
- Qual a média de resistência à tensão de cada amostra?
- Qual é o desvio padrão de resistência à tensão para cada temperatura? O aumento de temperatura parece influenciar a variabilidade de resistência à tensão?
- Em estatística, a amplitude é a diferença entre o maior e o menor valor de um conjunto de dados. Para cada temperatura, qual é a amplitude de resistência à tensão?
Passo 1
Fala galerinha!
Na letra a, a questão nos pede para calcularmos a média de resistência à tensão para cada temperatura de cura, então vamos usar a função mean().
Na letra b, devemos calcular o desvio padrão de resistência à tensão para cada temperatura, usando a função std(). Em estatística, o desvio padrão é um parâmetro que mede a variabilidade de uma amostra em relação à média. Quanto maior o desvio padrão, maior a variabilidade da amostra. Por isso, para vermos se o aumento da temperatura influencia a variabilidade, devemos comparar os desvios padrão que calculamos.
Na letra c, para encontrarmos a amplitude de resistência à tensão para cada temperatura, devemos usar as funções max() e min() e calcular a diferença entre os resultados de cada uma.
Depois de destrinchar o enunciado, bora resolver ;D
Passo 2
A primeira coisa que vamos fazer é entrar no Command Window dois vetores, um para cada coluna da tabela. Vamos fazer isso porque, pra usar os comandos de média, desvio padrão, mínimo e máximo, precisamos dos dados todos juntinhos num vetor (um pra cada temperatura).
T_20 = [2.07 2.14 2.22 2.03 2.21 2.03 2.05 2.18 2.09 2.14 2.11 2.02];
T_45 = [2.52 2.15 2.49 2.03 2.37 2.05 1.99 2.42 2.08 2.42 2.29 2.01];
O vetor T_20 contém os valores de resistência à tensão da primeira coluna da tabela, referente a 20 °C. Já o vetor T_45 contém os valores da segunda coluna da tabela, referente a 45 °C. Por enquanto, temos isso aqui no MATLAB:

Dica: coloquei o ; no final de cada comando para o MATLAB não imprimir o vetor logo depois de eu entrar com ele. Dessa forma, nosso Command Window fica menos poluído.
Agora vamos calcular a média de cada vetor. Para isso, vamos usar a função mean() duas vezes, uma em cada vetor:
media_20 = mean(T_20)
media_45 = mean(T_45)
A primeira linha de código acima vai retornar a média dos valores do vetor T_20 e armazenar a média em uma variável chamada media_20.
A segunda linha de código acima vai retornar a média dos valores do vetor T_45 e armazenar a média em uma variável chamada media_45. Note que ambas as linhas não têm o ; no final. Logo, o MATLAB vai imprimir pra gente o resultado no Command Window.
No MATLAB, ficou assim:

Portanto, a média de resistência à tensão para amostra submetida a uma temperatura de cura de 20 °C é 2,1075 Mpa.
Já a média para a amostra submetida a uma temperatura de cura de 45 °C é 2,2350 MPa. Dessa forma, a letra a está resolvida e podemos partir para a letra b.
Passo 3
Na letra b, devemos calcular o desvio padrão de cada amostra. Para isso, vamos usar a função std(). No Command Window, entre as duas linhas de código:
d_pad_20 = std(T_20)
d_pad_45 = std(T_45)
Na primeira linha de código, pedimos ao MATLAB que calcule o desvio padrão dos valores do vetor T_20 e armazene o desvio padrão em uma variável chamada d_pad_20.
Na segunda linha de código, pedimos ao MATLAB que calcule o desvio padrão dos valores do vetor T_45 e armazene o desvio padrão em uma variável chamada d_pad_45. O Command Window do MATLAB nos imprime essas respostas:

Portanto, o desvio padrão da amostra de 20 °C é de 0,0709 MPa e o desvio padrão da amostra de 45°C é de 0,2032 MPa.
A letra b da questão pede para refletirmos se o aumento da temperatura tem algum impacto na variabilidade da amostra. Podemos fazer essa reflexão a partir dos valores de desvio padrão que encontramos, já que o desvio padrão serve para avaliar a variabilidade de uma amostra. Quanto maior o desvio padrão, maior a variabilidade.
Repare que d_pad_20 é menor que d_pad_45, indicando que a amostra com temperatura de cura de 20 °C tem menor variabilidade quando comparada com a amostra com temperatura de cura de 45 °C. Logo, há indícios de que o aumento da temperatura aumenta a variabilidade de resistência à tensão.
Passo 4
Finalmente, vamos resolver a letra c. Para calcularmos a amplitude das amostras, devemos antes encontrar os valores máximo e mínimo de resistência à tensão de cada amostra. Para isso, vamos usar a função max(), para encontrar a maior resistência de cada coluna da tabela, e a função min(), para encontrar a menor. Vamos entrar as quatro linhas de código:
min_20 = min(T_20)
max_20 = max(T_20)
min_45 = min(T_45)
max_45 = max(T_45)
Na primeira linha de código, pedimos ao MATLAB que nos dê o menor valor do vetor T_20 e que o menor valor seja armazenado na variável min_20. Já na segunda linha de código, pedimos ao MATLAB que nos dê o maior valor do vetor T_20 e que o maior valor seja armazenado na variável max_20.
As linhas 3 e 4 fazem a mesma coisa, mas para o vetor T_45. Bora ver como fica no MATLAB:

Para calcular a amplitude de cada amostra, fazemos a diferença entre o valor máximo e mínimo de cada temperatura, por meio das duas linhas de código:
amp_20 = max_20 - min_20
amp_45 = max_45 - min_45
Na primeira linha, calculamos a amplitude para a amostra de 20 °C e armazenamos o resultado na variável amp_20.
Na segunda linha, calculamos a amplitude para a amostra de 45 °C e armazenamos o resultado na variável amp_45. Vamos ver a resposta que o MATLAB nos deu:

Temos que a amplitude de resistência à tensão para a amostra de 20 °C é de 0,2 MPa e que a amplitude para 45 °C é de 0,53 MPa.
Resposta
- A média de resistência à tensão para a amostra submetida a uma temperatura de cura de 20 °C é 2,1075 Mpa. Já a média para a amostra submetida a uma temperatura de cura de 45 °C é 2,2350 MPa.
- O desvio padrão da amostra de 20 °C é de 0,0709 MPa e o desvio padrão da amostra de 45°C é de 0,2032 MPa. Como o desvio padrão da amostra de 20 °C é menor do que o desvio padrão da amostra de 45°C, indicando que a amostra com temperatura de cura de 20 °C tem menor variabilidade, há indícios de que o aumento da temperatura aumenta a variabilidade de resistência à tensão.
- A amplitude de resistência à tensão para a amostra de 20 °C é de 0,2 MPa e a amplitude para 45 °C é de 0,53 MPa.
Exercício Resolvido #5
“UFSC - ENGR211 Help: MATLAB Exercises – Vetores e Matrizes. Exercício 6 (2021)”
Use o comando seguinte para criar uma matriz chamada :
![]()
- Calcule a média de cada coluna e atribua o resultado a um vetor .
- Calcule o desvio padrão de cada coluna e atribua o resultado a um vetor .
Passo 1
Neste exercício, criaremos uma matriz de linhas e colunas com números aleatórios. Resolveremos a letra a do exercício usando a função do MATLAB. Já letra b resolveremos com a função .
Passo 2
No Command Window do MATLAB, entre o comando dado pelo enunciado para a criar a matriz :
![]()
Este comando usa a função do MATLAB com duas entradas: o número de linhas e o número de colunas de uma matriz. Desta forma, é criada uma matriz composta por números aleatórios vindos da distribuição normal padrão. No comando acima, é criada uma matriz de linh e colunas que é armazenada na variável .
Passo 3
A letra a do exercício pede para calcularmos a média de cada coluna de e armazenar o resultado em um vetor chamado . Para isto, usaremos a função , que retorna a média aritmética de um conjunto de dados.
Até agora, usamos a função somente com vetores como entrada, mas ela também aceita matrizes. Quando a entrada de é uma matriz, ela retorna um vetor com a média de cada coluna da matriz. Legal, né? Desta forma, podemos resolver a letra a com uma única linha de código:
![]()
Com este comando, aplicamos na matriz . Como tem colunas, nos dará um vetor de elementos, correspondendo à média de cada coluna de . Este vetor é armazenado na variável , que é a resposta da letra a.
Passo 4
A letra b do exercício pede para calcularmos o desvio padrão de cada coluna de e armazenar o resultado em um vetor chamado . Para isto, usaremos a função , que retorna o desvio padrão de um conjunto de dados.
Assim como , a função também aceita matrizes como entrada. Quando a entrada de é uma matriz, ela retorna um vetor com o desvio padrão de cada coluna da matriz. Por isso, também podemos resolver a letra b com uma linha de código:
![]()
Com este comando, aplicamos na matriz . Como tem colunas, nos dará um vetor de elementos, correspondendo ao desvio padrão de cada coluna de . Este vetor é armazenado na variável , que é a resposta da letra b.
Para ter a resposta do exercício, imprima e no Command Window. Mas lembre: a sua resposta com certeza vai ser diferente da minha, pois os elementos da matriz são gerados aleatoriamente. Eles são diferentes a cada execução de código.
Resposta


Exercício Resolvido #6
“Adaptado de UERJ – Curso de MATLAB 5.1: Introdução à Solução de Problemas de Engenharia. Laboratório de Engenharia Elétrica. Aplicação em Solução de Problemas: Adaptador p/ Redução de Ruído, p. 141”
O adaptador para redução de ruído é um equipamento utilizado para reduzir o efeito de interferência de ruídos em um sinal. Por exemplo, um microfone que é utilizado para gravar sinais de voz de um grande auditório. Outro microfone é usado na parte de trás do auditório para colher principalmente os sinais de ruído. Através das técnicas para cancelamento de ruídos, as características do sinal de ruído podem ser determinadas usando o sinal de dois microfones. Os adaptadores são utilizados para reduzir o ruído oriundo da parte de trás do auditório, para poderem ser transmitidos para a sala de controle. Este processo resulta num sinal limpo e uma melhor comunicação.
Os algoritmos para os adaptadores estão acima do nível deste texto, mas a performance e a velocidade do algoritmo dependem das características dos sinais de entrada. Estas características determinam a superfície multidimensional quadrática para que obtenhamos um valor mínimo. Este mínimo é determinado ajustando o algoritmo para um ponto de partida para um único mínimo. Se a superfície quadrática tem um contorno circular, o algoritmo não é necessário. A matriz pode ser computada a partir dos sinais de entrada, e os autovalores da matriz irão determinar o tipo de superfície de contorno a ser utilizada. Se os autovalores forem iguais, a superfície é circular. Quanto maior a variação dos autovalores, mais elíptica será a superfície. Os autovetores representam o eixo principal da superfície. Portanto para determinar a velocidade e a performance do algoritmo do adaptador com certeza do tipo de dados e para analisar a superfície, nós precisamos determinar os autovalores e autovetores da matriz .
Escreva um programa para ler os valores da matriz , e depois calcule os autovalores e autovetores.
Passo 1
O exercício traz um textão para dar uma contextualização, mas basicamente o que ele quer é que calculemos os autovalores e os autovetores da matriz . Faremos isso por meio da função do MATLAB.
Passo 2
Entre com a matriz no MATLAB:

Em seguida, aplicaremos a função em . A função tem a sintaxe:
Ela tem como entrada uma matriz quadrada e nos retorna as matrizes e . As colunas da matriz são os autovetores de e a matriz é uma matriz diagonal com os autovalores de . Portanto, em seu script, adicione o comando:
![]()
A matriz terá os autovetores de e a matriz , os autovalores. Execute o comando acima para ver e :

Passo 3
A partir do texto do enunciado, podemos interpretar o resultado. Temos que os autovetores de são:
e
E os autovalores de são e . Como os autovalores não são iguais, a superfície quadrática não possui um contorno circular, o que fará com que a performance do adaptador será lenta e menos precisa.
Este exemplo é bem simples, com uma matriz . Mas, por exemplo, se estivéssemos trabalhando com comunicação com satélites, a matriz teria milhares de linhas de colunas e teríamos que usar outros comandos para verificar a igualdade dos autovalores.
Resposta
Os autovetores de são:
e
Os autovalores de são e .
Exercício Resolvido #7
“Adapado de UnB - Laboratorio de Análise Dinâmica Linear. Experimento 01 - primeira parte. Simulação de Sistemas Dinâmicos Lineares/Visãoo Geral do Matlab. Exercício 3 (2017)”
Considere um motor a pistão em uma aeronave. Durante o seu funcionamento, um sensor de temperatura registrou os seguintes dados:

Determinar o valor máximo, mínimo e médio da temperatura em graus Celsius.
Passo 1
Neste exercício, entraremos no MATLAB os dados de temperatura da tabela. Em seguida, converteremos as temperaturas de °F para °C implementando a fórmula de conversão de temperatura dada pelo enunciado.
Após a conversão, usaremos os comandos , e para encontrar a temperatura máxima, a tempertura mínima e a média de temperatura, respectivamente.
Passo 2
Primeiramente, vamos entrar com os dados de temperatura em °F da tabela no MATLAB, armazenando-as em um vetor chamado :

Passo 3
Após entrar com o vetor com as temperaturas, podemos criar outro vetor com as temperaturas em °C, usando a fórmula do enunciado. Este vetor se chamará e é definido a partir do comando:
![]()
Este comando usa a fórmula de conversão do enunciado, aplicando-a ao vetor . Desta forma, o vetor contém as temperaturas de convertidas para °C.
Passo 4
Com o vetor , calculamos a temperatura máxima, a temperatura mínima e a temperatura média.
Para encontrar a temperatura máxima em °C, vamos aplicar a função em , que retorna o valor máximo de um conjunto de dados:
![]()
A temperatura máxima é armazenada na variável .
Para encontrar a temperatura mínima em °C, vamos aplicar a função em , que retorna o valor mínimo de um conjunto de dados:
![]()
A temperatura mínima é armazenada na variável .
Finalmente, para calcular a média das temperaturas, aplicaremos a função em , que calcula a média aritmética de um conjunto de dados:
![]()
A média das temperaturas é armazenada em .
Para ver o valor máximo, mínimo e médio da temperatura em °C, execute o programa e imprima e no Command Window:

Resposta
A temperatura máxima é
A temperatura mínima é
A média de temperatura é