Programação: Algoritmos e a Janela New script.
Teoria
Opaaaaa, iae tudo ok?
Hoje iremos começar um novo bloco que é o bloco de programação.
Nesse primeiro momento vamos conversar sobre alguns aspectos gerais e bater um papo mais específico sobre os algoritmos e algumas terminologias usadas dentro da área de programação, em conjunto com a aba New Script que é o ambiente de programação do Matlab.
Primeiramente precisamos conhecer a diferenciação entre rotina, sub-rotina e função para a programação, então vamos lá.
Rotinas e algoritmos
Antes de qualquer coisa vamos imaginar que você precisa ir ao mercado comprar frutas para sua despensa.
Então, seu problema é ir na seção de frutas e selecionar algumas que você julgue estarem boas para consumo, belezinha?
Com isso, o passo a passo que você provavelmente vai realizar é o seguinte:
- Pegar a fruta.
- Cheirar a fruta.
- A fruta tem cheiro estragado?
- Se a resposta for Sim: Devolve a fruta para seu lugar e vai para o passo 1
- Se a resposta for Não: Coloca a fruta no carrinho e vai para o passo 4
- Completou a quantidade de frutas que queria?
- Se a resposta for Sim: Segue para o passo 5.
- Se a resposta for Não: Repete o ciclo a partir do passo 1
- Encerrar compras, pagar e ir embora.
Esse passo a passo que você está realizando é o que chamamos de rotina, aqui temos uma rotina para a compra e seleção de frutas, que de forma geral não passa de um conjunto de informações e ferramentas sequenciadas para que você consiga resolver o seu problema, que nesse caso é comprar as frutas.
Além disso, você também pode ouvir falar das sub-rotinas, que são partes de uma rotina, no nosso exemplo, podemos dizer que o passo onde decidimos se a fruta tá boa ou não é uma sub-rotina.
Dentro da rotina, a estrutura sequencial, quer dizer, o passo a passo descrito é o que chamamos de algoritmo.
E ao longo do dia, você sem perceber executa vááários algoritmos e rotinas nas suas tarefas!
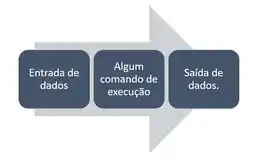
Agora vamos dar uma olhada mais a fundo no algoritmo que criamos, podemos perceber os seguintes elementos nele:
Primeiramente a entrada de dados: pegar uma fruta.
Depois, temos um comando de execução: no exemplo, é cheirar a fruta e avaliar se a fruta está boa ou não.
E por fim, temos uma saída de dados: que é colocar a fruta no carrinho ou deixar na prateleira do mercado.
E qualquer rotina que você imaginar segue esse mesmo passo a passo:
Por isso, para escrever qualquer algoritmo, primeiramente esses elementos precisam estar bem claros.
Bem, agora que vimos o que é o algoritmo, devo te informar que existem duas formas de representá-lo: a primeira é através de texto como foi visto, e a segunda é utilizando uma forma gráfica chamada de diagrama de blocos.
Geralmente o diagrama de blocos é mais utilizado por ser uma representação mais elegante e visualmente mais fácil de entender o que está acontecendo no código.
Por exemplo vamos colocar o exemplo da compra de frutas no diagrama de blocos:
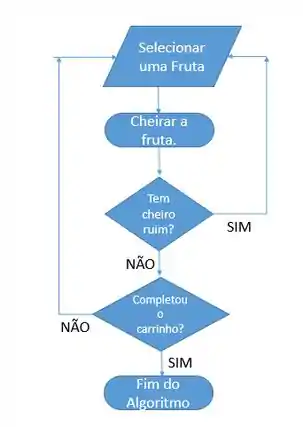
Para a elaboração desses diagramas de blocos existem diversas regras sobre como organizar e quais bloquinhos usar, porém, para a elaboração de algoritmos simples precisamos apenas lembrar o que o losango é o componente para as tomadas de decisão, a entrada de dados é dada pelo paralelogramo e a saída é dada por essa elipse ‘achatadinha’ que indica o fim do algoritmo.
Eu sei que essas regras podem ser chatinhas, porém, a visualização do algoritmo assim fica bem mais clara.
O que você acha?
Funções e a Janela New Script
Opa, agora é hora de levarmos essa conversa pro Matlab!
Uma função é uma sequência de comandos que vai executar uma tarefa específica dentro do seu programa, elas são muuuito parecidas com as sub-rotinas.
Bem, para começarmos a falar das funções vamos falar sobre a aba new script.
Primeiramente abra o Matlab e você estará na janela inicial, logo após você irá clicar no botão que é o primeiro botão da barra de ferramentas.
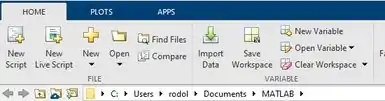
A depender da versão pode mudar um pouco, como minha versão é a 2021 minha janela irá ficar assim:
Ficarão abertas simultaneamente duas abas, uma é a aba editor e a outra é uma amiga bem antiga, que é a command Window.
A nossa pop star do momento a partir de agora será a aba editor e a command window se tornará nossa coadjuvante. Bem, agora vamos ver a sintaxe de como definir uma função no Matlab com um exemplo simplesinho, okay?
Vamos criar a seguinte função no Matlab:
.
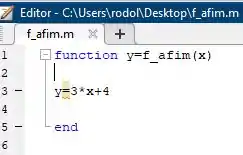
Para isso devemos escrever na aba edit assim
Após isso, salve o arquivo em algum lugar. Obs: Salve com o nome da função, nesse caso vou chamar de , pois o Matlab exige que o Arquivo e a função tenham o mesmo nome.
Se você fez tudo certinho, o Matlab deve mostrar para você na barra edit algo assim:
Agora que você salvou, vá na command Window logo abaixo do edit e digite:
Você deve ver algo assim:
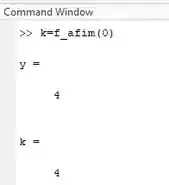
Antes estávamos limitados apenas a funções existentes no Matlab, agora o nosso leque de opções cresce indefinidamente e podemos calcular as mais diversas funções existentes em qualquer área das ciências exatas!
Para finalizar de uma forma geral a sintaxe de uma função no Matlab fica:
“Código da função”
Bem, já comi bastante do tempo de vocês e vou ficando por aqui.
Ahh não se esqueça dos exercícios okay? Tem uns exercícios bem legais dessa parte de função. Pois a programação é prática, ou seja, quanto mais você praticar melhor ainda você se torna!
Obrigadooo e até a próxima!
Funções e a Janela New Script
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Seja uma função de primeiro grau dada por:
Elabore um algoritmo para o cálculo das raízes da função de primeiro grau a partir dos coeficientes a e b da função.
Passo 1
Opa, está tudo bem?
De uma forma direta o enunciado pede a elaboração de um algoritmo para o cálculo dos zeros da função afim. Onde a entrada de dados seja unicamente os coeficientes e da função.
Um algoritmo é um conjunto de passos que devem ser seguidos para fazer um cálculo, ou seja, é um procedimento. São os comandos que devem ser dados do programador para a máquina.
Passo 2
Para o cálculo dos zeros da função afim a equação que será utilizada é deduzida fazendo y=0, então temos que:
Logo
Ou seja, é preciso obter os valores de a e b, calcular o x e retornar a resposta pro usuário.
Sendo assim a sequência de passos para o cálculo dessa raiz é dada por:
- Entrada de dados: a e b
- Cálculo da Raiz com a equação:
- Saída de dados:
Passo 3
Observando a representação escrita do algoritmo desenvolvida no segundo passo conseguimos ver que o algoritmo não precisa de um teste lógico, então o fluxo de informação tem um sentido contínuo.
Logo temos um bloco para a entrada de dados, um segundo bloco para o cálculo do X e finalizamos com o bloco de saída de dados.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
Elaboração Própria
Seja uma função de primeiro grau dada por:
Com diferente de 0.
Elabore em Matlab um código para que se permita verificar o zero da função.
Passo 1
A questão em si quer utilizar a janela new script para que se possa realizar a elaboração de um código em matlab que a partir dos coeficientes da função afim.
A ideia aqui é criar uma função no matlab que permita isso utilizando a função function, para que assim se possa aumentar ainda mais o leque de possibilidade utilizando o Matlab.
Passo 2
Para encontrar a raiz da equação afim precisa fazer na equação
Resultando em:
Sendo assim nós temos na função duas entradas, montando o algoritmo de forma rápida e simples temos:
1-Entrada de dados: e
2-Cálculo do
3-Saída de dados
Logo no Matlab a função criada tem dois argumentos, precisando escrever da seguinte forma
function x=raiz(a,b)
X=-b/a
end
Salvando como o arquivo raiz, deve lhe mostrar algo assim:
Passo 3
Vamos realizar um teste, vamos calcular a raiz da função afim
Que é x
Utilizando nosso código, com b=2 e a = 5 temos:
o Matlab deve mostrar:
OBS: Sempre inserir as variáveis na ordem que definir. Na função disse que a primeira variável é o coeficiente angular e a segunda é o coeficiente linear.
Se caso em vez de escrever e escrever a function vai entender que 2 é o coeficiente angular e 5 o coeficiente linear como mostrado abaixo.
Então sempre lembrar, a ordem de qual variável é qual segue a ordem que você definiu no código, beleza?
Esse exercício te ajudou? Responde Ai.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #3
Elaboração Própria
Ganeff é um estudante de engenharia química que se deparou com um dos problemas mais chatinhos da engenharia química que é converter a fração mássica em fração molar.
Olhando na literatura ele encontrou a seguinte fórmula:
Elabore em Matlab um código no qual converte a fração mássica em fração molar para uma mistura de 3 componentes, onde é a massa molecular do composto e é sua respectiva fração mássica.
Passo 1
Esse tipo de coisa com quem é da área de engenharia é bem chatinho, aposto que todo mundo já se deparou com um exercício que precisa os valores em base molar e a questão te dá em base mássica.
Bem a questão quer que elabore um código utilizando a janela new script que converte as frações mássicas em frações molares para uma mistura de 3 componentes, logo teremos 3 frações mássicas para converter em fração molar
A ideia é criar uma function no Matlab que faça esse trabalho todo automatizando essas contas, entende?
Passo 2
Então vamos lá, antes de começar a programar é legal escrever um algoritmo rápido para que se possa enxergar o passo a passo que seu código precisa fazer.
1-Entrada de dados ()
2-Cálculo dos denominadores:
3- Cálculo das frações:
Sendo assim, a function fica
function x=molar
end
(OBS: Coloquei o “;” no D porque o que me interessa é apenas as composições para não ficar imprimindo ele direto).
Digitando tudo certinho e salvando o arquivo deve aparecer algo assim na sua tela;
Passo 3
Aqui você pode pegar qualquer mistura, mas na hora de chamar a função os argumentos de entrada precisam estar na mesma ordem que você definiu.
Vamos lá, eu escolho:
Componente (1) é a Água, w=0,2 e M=18 g/mol
Componente (2) é o Etanol, w=0,5 e M=46 g/mol
Componente (3) é o Ciclo-Hexano, w=0,3 e M=84,16 g/mol
Escrevendo no command Window na mesma ordem que foi definida na function temos:
Que nos irá retornar:
Agora você tem um conversor de fração mássica em molar todo automatizado.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #4
Elaboração Própria
Em geral para problemas de Física a conversão de unidades se torna uma tarefa árdua, sendo assim, um aluno do curso de física através da literatura encontrou funções de primeiro grau que servem para converter entre as escalas de temperatura, essas funções são as:
Elabore uma Rotina em Matlab que converta a Temperatura em graus Celsius nas demais escalas.
Dica: Note que vai sair mais de uma temperatura, então a saída da função é um vetor, então na hora de definir a function vai ficar function [X1 X2 X3] invés de ser apenas y=function.
Passo 1
Opa a questão em si pede para montar um programinha que converte as temperaturas, que em geral é algo chatinho de se fazer de forma manual, então se você consegue automatizar isso já é uma ajuda grande na nossa carreira universitária.
Enfim, gostaria de falar da dica porque a entrada da função é a Temperatura em graus Celsius então estamos entrando com um valor qualquer, ou seja, um escalar.
Já a saída é um Vetor porque você tem 3 Temperaturas, então na hora de implementar a função precisa indicar que a variável de saída é um vetor, ok?.
Isso vai ficar claro já já
Passo 2
Antes de escrever qualquer coisa vamos escrever um pequeno algoritmo para que nós possamos nos orientar sobre o que nosso programa irá fazer.
1-Entrada de dados( T)
2-Cálculo das temperaturas(TRank,Tkelvin,TFare)
3-Impressão das Temperaturas no Command Window
Uma vez feito isso, podemos perceber que nosso código, a nossa function fica:
Se escreveu tudo direitinho, deve ficar algo assim:
Passo 3
Agora que conseguimos escrever o código vamos realizar um testezinho, Vamos calcular a Temperatura para T=25 °C. Os valores devem em Kelvin deve dar 298,15 digitando no command window temos:
OPAAAAAAAAAAAAA agora temos um conversor de escala de temperaturas prontinho para te ajudar nas disciplinas
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #5
Elaboração Própria
Dado que a equação de segundo grau é dada por:
Elabore um algoritmo para a solução da equação de segundo grau que unicamente depende dos coeficientes a,b e c da equação e além disso verifique e mostre se as soluções são reais, complexas ou iguais.
Obs: Represente na forma escrita e também na forma de diagrama de blocos. Quando falo em mostrar é imprimir como uma saída de dados o tipo da solução.
Passo 1
A ideia da questão é mostrar como pensar para a realização de algoritmos mais complexos e para a criação de programas mais avançados.
O problema em si pede a elaboração de uma rotina (do passo a passo) para o cálculo das soluções da equação de segundo grau, ou seja, um algoritmo.
Esse problema está intimamente relacionado com os alunos e esse passo a passo é realizado quase de imediato sem que os mesmos percebam, então o que vamos fazer aqui é apenas colocar no papel o que você faz toda vez que resolve uma equação de segundo grau.
Passo 2
Para a resolução de uma equação de segundo grau, precisamos de 2 equações:
Onde a,b,c são chamados de coeficientes da equação e o é o discriminante da equação de segundo grau.
O discriminante tem um papel fundamental para nosso algoritmo, pois ele é o parâmetro que vai qualificar qual é o tipo das nossas soluções.
- Se Temos raízes complexas conjugadas
- Se Temos duas raízes iguais
- Se Temos duas raízes Reais distintas
Sendo assim vamos começar a escrever o algoritmo.
- Entrada de dados: a,b,c
- Cálculo do discriminante:
- Cálculo do e
- Saída de dados e ,
2.1 – Se
imprima “Temos raízes complexas conjugadas”
2.2- Se
imprima”Temos duas raízes iguais”
2.3 – Se
imprima”Temos duas raízes Reais distintas”
Passo 3
Utilizando o algoritmo desenvolvido no passo 2 é possível gerar o diagrama de blocos abaixo:
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #6
Autoria Própria
Um sistema de equações lineares do tipo:
Pode ser resolvido segundo as equações:
Escreva um algoritmo que lê os coeficientes e calcula e mostra os valores de
Passo 1
Opa galera aqui é uma questão puramente teórica de elaboração de algoritmos.
Os algoritmos são a base da programação é a partir deles que rotinas são elaboradas, seja das mais complexas até as mais simples.
É nele que o programador vai colocar suas ideias e vai definir os caminhos de informações e as devidas operações que seu código irá realizar.
O enunciado pede para desenvolver um algoritmo para o cálculo de um sistema de equações.
A ideia aqui é partir de uma entrada de dados para inserir os coeficientes realizar as operações desejadas e finalizar com a saída de dados.
Passo 2
Primeiramente precisamos implementar a entrada de dados que é a base de todo o programa.
Você consegue somar dois números sem saber que números são esses?
Ou você consegue ir ao mercado comprar algo sem nem saber o que precisa comprar?
Bem, acredito que não, né? Todo programa precisa de algumas informações mínimas para ele desenvolver seus cálculos e essas informações são as chamadas entradas de dados.
E nossa entrada de dados nesse problema é justamente os coeficientes do sistema de equações de segundo grau, pois é com eles que podemos calcular os valores de
Após a entrada de dados precisamos realizar as operações de cálculo, que são as equações de dadas no problema.
E para finalizar precisamos que o programa nos mostre os valores que ele calculou né?
Imagina só você ir na padaria pedir 10 pães, ai o padeiro te entrega um saco mas você não pode abrir e nem contar.
É meio sem sentido né?
Então vamos colocar a nossa saída de dados, a nossa saída é justamente os valores que queremos saber que é o e o .
Passo 3
Logo o nosso algoritmo se torna:
As linhas de fluxo ficam, entrada de dados onde nós coletamos as entradas e depois calculamos os valores de e e por último o programa imprime os valores deixando as linhas de fluxo de sinais dessa forma, saindo do quadro anterior e entrando no próximo.
Resposta
Exercício Resolvido #7
Autoria Própria
Elabore um algoritmo que calcule a média aritmética das 3 notas de um aluno e mostre, além do valor da média, uma mensagem de "Aprovado", caso a média seja igual ou superior a 6, ou a mensagem "reprovado", caso contrário
Passo 1
Opa galera aqui é uma questão puramente teórica de elaboração de algoritmos.
Os algoritmos são a base da programação é a partir deles que rotinas são elaboradas, seja das mais complexas até as mais simples.
É nele que o programador vai colocar suas ideias e vai definir os caminhos de informações e as devidas operações que seu código irá realizar.
O enunciado pede para desenvolver um algoritmo para o cálculo de um sistema de notas para um aluno.
Realizamos esse tipo de operação diversas vezes sem nem perceber, quem aqui nunca chegou no final do período para fazer a contagem dos pontos para ir para final? KKKKKK
A ideia aqui é partir de uma entrada de dados que corresponde às três notas do aluno e realizar as operações que se deseja.
Aqui temos duas operações, a primeira é uma operação aritmética que vamos utilizar para calcular o valor da média.
A segunda operação é um teste lógico, pois, o aluno será aprovado se sua média for superior a 6 e reprovado caso contrário.
Ficou claro? Se sim, vamos nessa.
Passo 2
Primeiramente vamos começar o programinha do início que é a entrada de dados.
A entrada de dados é onde toda a história começa, você já foi ao supermercado comprar comida sem nem ao menos saber o que está faltando na sua dispensa?
Acredito que não, né? Então aqui é igual. O programa não irá fazer nada se não dermos algumas informações mínimas que aqui correspondem às três notas do aluno, belezinha?
Agora que já implementamos as 3 notas precisamos realizar a operação aritmética que é o cálculo das médias para poder saber que o carinha foi aprovado ou não.
Agora que calculamos a média, precisamos saber se o nosso compatriota foi aprovado ou não, para isso vamos precisar de uma estrutura de decisão popularmente chamada de teste lógico.
Agora que implementamos o teste lógico vamos implementar as suas respostas.
O fluxo da informação é que nós inserimos a entrada de dados, após isso vamos calcular a média para depois tomar uma decisão se ele está aprovado ou não.
Sendo assim, nosso algoritmo se torna:
Resposta
Exercício Resolvido #8
Autoria Própria
Elabore um algoritmo que dada a idade de um nadador classifica-lo em uma das seguintes categorias
Infantil A = 5 – 10 anos
Juvenil A = 11- 17 anos
Adulto = maiores de 18 anos
Passo 1
Opa galera aqui é uma questão puramente teórica de elaboração de algoritmos.
Os algoritmos são a base da programação é a partir deles que rotinas são elaboradas, seja das mais complexas até as mais simples.
É nele que o programador vai colocar suas ideias e vai definir os caminhos de informações e as devidas operações que seu código irá realizar.
O enunciado pede para elaborar um algoritmo que classifique o competidor de natação em função da sua idade.
Para elaboração desse algoritmo iremos precisar de uma entrada de dados que nesse exercício é a idade do competidor.
Após a entrada de dados, vamos precisar de uma série de testes lógicos a fim de classificar o competidor em alguma classe disponibilizada pelo enunciado.
Passo 2
Primeiramente vamos começar o programinha do início que é a entrada de dados.
A entrada de dados é onde toda a história começa, você já foi ao supermercado comprar comida sem nem ao menos saber o que está faltando na sua dispensa?
Acredito que não, né? Então aqui é igual. O programa não irá fazer nada se não dermos algumas informações mínimas que aqui correspondem a idade do competidor, belezinha?
Agora que conseguimos implementar a entrada de dados vamos implementar os testes lógicos. A ordem dos testes vou escolher de forma arbitrária seguindo a idade, pois isso não interfere em nada na resposta final.
Primeiro teste pergunta se a idade do competidor que vamos chamar de idade está contida no intervalo:
Se a resposta for sim o competidor se classifica como infantil A caso contrário ele irá para o próximo teste lógico e assim sucessivamente.
O segundo intervalo pergunta se a idade está entre 10 e 17, se estiver o competidor é classificado como juvenil, caso contrário precisa-se ir para o próximo teste.
E finalizamos com o último caso que é para aqueles que são maiores de 18 anos que são classificados como adultos.
Passo 3
Logo, unificando cada parte temos:
Resposta
Ei, a resposta está no passo a passo :)