EDOs no SIMULINK
Produzido por Gustavo BarbosaTeoria
Introdução
E aí, tudo joia? Na aula de hoje vamos aprender como resolver equações diferenciais ordinárias (as EDO’s) no SIMULINK. Se você não se lembra o que é uma EDO, vamos fazer uma revisão vapt-vupt (lembrando que no Responde Aí temos aulas só sobre EDO’s, caso você queira dar uma revisada mais profunda).

Uma EDO é uma equação que envolve uma função, suas derivadas e uma variável independente. Uma EDO de primeira ordem é uma equação desse estilo:
onde é uma variável independente. A solução de uma EDO é a função da equação, no caso, . Para encontrar , integramos e definimos uma condição inicial para termos uma única solução.
Em uma EDO de primeira ordem, a derivada de maior ordem é a primeira derivada da função. Se uma EDO tem uma derivada segunda, ela é de segunda ordem, e assim por diante.
Resolver EDO’s no SIMULINK permite construir modelos intuitivos representando a EDO e gerar facilmente muitos gráficos além da solução da EDO (por exemplo, além de plotar a função, plotar suas derivadas).
Lembra que eu disse que integramos a derivada da função para encontrá-la? O SIMULINK tem um bloco que faz a integração de um sinal, o “Integrator”.
O bloco “Integrator”
O bloco “Integrator” pertence à biblioteca “Continuous”:
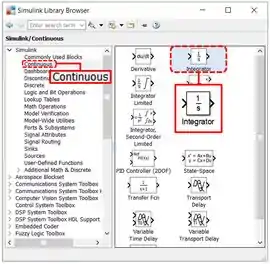
Note que o símbolo do bloco é . Isso porque quando fazemos a transformada de Laplace de uma integral, ela é transformada em .
Dentre os parâmetros do bloco “Integrator”, está a condição inicial, destacada em vermelho abaixo (“Initial Condition”):
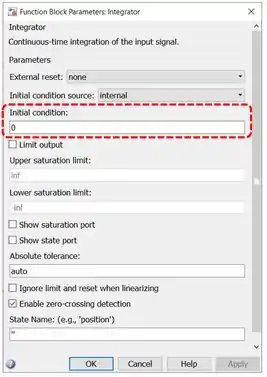
Por padrão, as condições iniciais são nulas. O bloco possui outras propriedades, mas o parâmetro das condições iniciais é o que mais vamos mexer.
E como modelamos uma EDO no SIMULINK? Vamos pegar como exemplo a EDO:
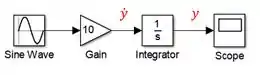
Queremos encontrar , considerando condições iniciais nulas. Vamos começar modelando a parte direita da EDO, por isso, adicionamos um bloco “Sine Wave” e um bloco “Gain”, com ganho igual a , em série em um modelo do SIMULINK:

Blocos em série representam multiplicação, logo, os dois blocos acima representam . E é igual a quê? A derivada ! Logo, o sinal de saída do diagrama acima é , como indicado em vermelho acima (o diagrama deu spoiler).
Para encontrar , precisamos integrar , por isso adicionamos o bloco “Integrator” logo à direita do “Gain”. A saída de “Integrator” será o resultado da integral de , isto é, . Podemos incluir um “Scope” como saída, para fecharmos o diagrama de blocos:
Um “macete” para modelar uma EDO com os blocos do SIMULINK é tentar isolar a derivada de maior ordem na equação, mais ou menos como pensar: “a derivada é igual a o quê?”. Dessa forma, você consegue identificar qual será a entrada do seu modelo, isto é, qual bloco da biblioteca “Source” você vai pegar (“Step”, “Sine Wave”, etc) e em qual ponto (ou quais pontos, como veremos mais pra frente) colocar o “Integrator”.
Vamos ver um exemplo um pouquinho mais complexo. Vamos resolver a EDO:
Com , para .
Já temos a derivada “isolada”: sabemos que é igual a . Já podemos também identificar a entrada do modelo: . Por isto, em um modelo em branco no SIMULINK, começamos inserindo um bloco “Sine Wave” e alteramos seus parâmetros “Amplitude” para e “Frequency” (frequência) para :
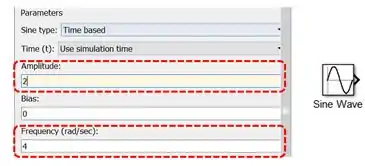
É a soma de com que resulta em , logo, inclua um bloco “Add” ao modelo e conecte o bloco “Sine Wave” a uma de suas entradas. Aproveite para já alterar o parâmetro “List of signs” (destacado abaixo), para uma das entradas de “Add” ter um sinal de menos, indicando que ele fará uma subtração.

A saída de “Add” será , por isso podemos incluir um “Integrator” e conectá-lo à saída de “Add”. Vamos aproveitar e já alterar a condição inicial para :

A saída de “Integrator” será , como indicado acima. Para incluirmos os blocos representando o termo , precisamos pôr um bloco de saída do modelo para receber e, em seguida, criar uma ramificação entre o bloco “Integrator” e o bloco de saída, para pegarmos , multiplicá-lo por e levá-lo à entrada com sinal de “Add”.
Vamos usar um bloco “Scope” como saída. Em seguida, inserimos um bloco “Gain” e fazemos que seu ganho é igual a :

Dica: você pode rotacionar os blocos no SIMULINK em sentido horário selecionando-os e apertando “Ctrl+R”.
Clique na entrada de “Gain” e conecte-a à flecha entre “Integrator” e “Scope”. Para fazer isto, clique sobre a entrada de “Gain” e arraste. Aparecerá uma flecha vermelha tracejada, você deve conectar a extremidade livre dessa flecha na flecha entre “Integrator” e “Scope”:
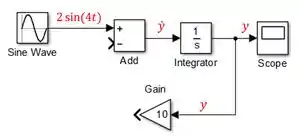
Desta forma, além de “entrar” no “Scope”, ele está sendo “levado” para ser multiplicado pelo ganho de “Gain”.
Para finalizar, conecte a saída de “Gain” à entrada de “Add” restante:

Este é o modelo do SIMULINK da EDO . Alterando o tempo de simulação para e executando a simulação, podemos ver o gráfico de :
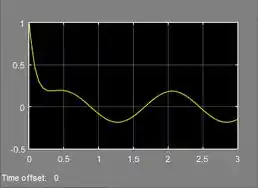
EDO’s de ordem superior
Para modelarmos EDO’s de ordem superior, como de segunda ordem, usaremos blocos “Integrator” em sequência:

Como exemplo, vamos modelar a EDO de segunda ordem:
Com condições iniciais nulas.
O primeiro passo é isolar a derivada de maior ordem, isto é, . Desta forma, temos que .
A entrada do modelo será um bloco “Constant” igual a , o qual será somado a e para gerar . Por isso, também usaremos um bloco “Add”, cuja saída será .
O sinal entrará em um bloco “Integrator”, para gerar , que entrará em outro “Integrator” para criar . Desta forma, tem-se o modelo da EDO de segunda ordem abaixo:

O diagrama acima tem as indicações do sinal de saída de alguns blocos, para ajudar a entender como ele representa a EDO.
Deu para perceber que a construção de modelos de EDO’s no SIMULINK é bem intuitiva. Existem algumas estratégias que você vai pegando com o tempo, por isso, tem que praticar bastante! Não deixe de fazer os exercícios que preparei, para ficar craque em modelar EDO’s no SIMULINK ;D
O bloco “Integrator”
EDO’s de ordem superior
Exercícios Resolvidos
Exercício Resolvido #1
“Adaptado de UFG & UCG – EEEC – Introdução ao Programa MATLAB com Aplicações, de Antônio César Baleeiro Alves, Enes Gonçalves Marra e José Wilson Lima Nerys. Exemplo 11.1, p. 61 (2007)”
Considere . Seja a equação diferencial de primeira ordem em , com valor inicial conhecido, .
Resolva a equação diferencial utilizando o SIMULINK.
Passo 1
Para resolver uma equação diferencial pelo SIMULINK, a dica é “isolar” a derivada da EDO. Por isso, vamos rearranjar a EDO para:
Desta forma, conseguimos fazer aquele raciocínio: “a derivada é igual a quê?” e descobrimos onde pôr o bloco “Integrator” para obter . Além do mais, isso ajuda a identificar qual o primeiro bloco que colocaremos no modelo, que muito provavelmente virá da biblioteca “Source”.
A resposta do exercício será um gráfico de , por isso, usaremos no modelo um bloco “Scope”.
Passo 2
Olhando a EDO rearranjada, sabemos é igual a , por isso, vamos começar modelando essa diferença, o lado direito da equação. Em um novo modelo, insira um bloco “Constant” e faça com que ele seja igual a . Em seguida, insira um bloco “Add” e altere o parâmetro “List of signs” (destacado abaixo), para que ambas as entradas de “Add” tenham um sinal negativo, para fazermos .

Passo 3
O objetivo é que a saída de “Add” seja igual a . E quem é ? É ! Logo, é à direita de “Add” que incluiremos um bloco “Integrator”, que nos dará . Para isto, vá à biblioteca “Continuous”, insira um bloco “Integrator” ao modelo e conecte sua entrada à saída de “Add”, como na figura abaixo:

Não sei se você reparou, mas eu anotei ali no modelo, acima da flecha entre “Add” e “Integrator”, um , pra dizer que aquele sinal é a derivada de . Você pode fazer isso clicando no botão “Annotation” (destacado em azul acima), na lateral esquerda da janela onde construímos os modelos, e em seguida clicando sobre o lugar onde você quer fazer a anotação. Daí, é só digitar o que você quiser.
Esse é um jeito bom de não se perder nos diagramas de blocos das EDOs.
Vamos alterar a condição inicial para , acessando as propriedades de “Integrator” e mudando o parâmetro “Initial Condition” de para :

Passo 4
A saída de “Integrator” será , a solução da nossa EDO. Como queremos gerar o gráfico dela, vamos inserir um bloco “Scope”. Conecte a saída de “Integrator” a entrada de “Scope”:

Agora que temos , podemos criar a componente da expressão . Para isto, insira um bloco “Gain”, da biblioteca “Math Operations”, altere seu ganho para e conecte sua entrada ao sinal saindo de “Integrator”. Você fará isto clicando sobre a entrada de “Gain” e arrastando. Aparecerá um flecha vermelha:
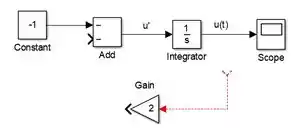
Conecte a extremidade livre à seta entre “Integrator” e “Scope”. Desta forma, vai para “Scope” e “Gain” simultaneamente. Em seguida, conecte a saída de “Gain” à entrada disponível de “Add”. Você estará levando para fazer a diferença :
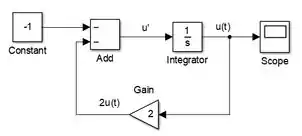
Pronto! A EDO está modelada no SIMULINK e podemos obter sua solução, em forma de gráfico, rodando o programa.
Resposta
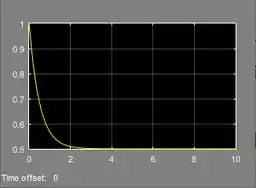
Exercício Resolvido #2
“Adaptado de UFG & UCG – EEEC – Introdução ao Programa MATLAB com Aplicações, de Antônio César Baleeiro Alves, Enes Gonçalves Marra e José Wilson Lima Nerys. Exemplo 11.3, p. 66 (2007)”
Considere o circuito elétrico abaixo:
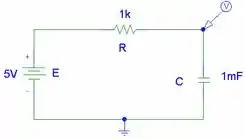
O circuito possui um resistor e um capacitor em série alimentados por uma fonte constante. O capacitor possui tensão inicial .
A equação diferencial que modela o circuito RC é:
Deseja-se obter a resposta para , por meio do SIMULINK.
Passo 1
O exercício pede encontrarmos solucionado a EDO que modela o curcuito RC usando o SIMULINK. Uma dica para resolver uma EDO pelo SIMULINK é deixar a derivada isolada no lado esquerdo da equação. Por isso, vamos rearranjar a EDO para:
Com isso, identificamos a expressão que é igual à derivada, montamos o diagrama de blocos que a representa e, na saída desse diagrama, incluímos um bloco “Integrator” para ter . Este será conduzido a um bloco “Scope”, para vermos seu gráfico.
Passo 2
Sabendo que , e , a EDO se torna:
Logo, é igual a . Vamos começar modelando essa diferença. Em um novo modelo, insira um bloco “Constant” e faça com que ele seja igual a . Em seguida, insira um bloco “Add” e altere o parâmetro “List of signs” (destacado abaixo) para , de forma que “Add” tenha uma entrada positiva e outra negativa. Conecte “Constant” à entrada positiva:

Passo 3
A saída de “Add” será igual a , que é igual a . Por isso, colocaremos à direita de “Add” um bloco “Integrator”, para obter . Para isto, vá à biblioteca “Continuous”, insira um bloco “Integrator” ao modelo e conecte sua entrada à saída de “Add”, como na figura abaixo:
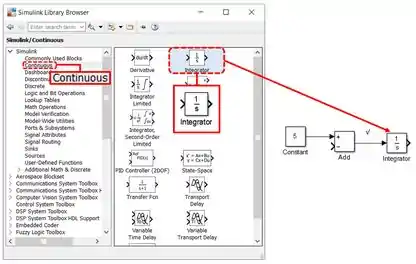
Precisamos mudar a condição inicial para . Acesse as propriedades de “Integrator” e altere o parâmetro “Initial Condition” de para :

Passo 4
A saída de “Integrator” será , a solução pedida pelo enunciado. Para gerar o gráfico dela, insira um bloco “Scope” e conecte a saída de “Integrator” à entrada de “Scope”:
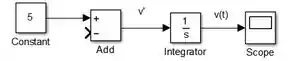
Leve para a entrada negativa de “Add”, para concluir a diferença . Para isto, clique sobre a entrada negativa de “Add” e arraste. Aparecerá uma flecha vermelha tracejada, cuja extremidade livre você deve conectar à seta entre “Integrator” e “Scope”:
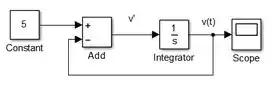
Pronto! Já montamos o diagrama de blocos que nos dará . Paa ver a curva de , execute o programa e clique duas vezes sobre o bloco “Scope”.
Resposta

Exercício Resolvido #3
“Adaptado de MATLAB for Engineering Applications, de William J. Palm III. Seção 10.2, exercício 6, p. 443”
A seguinte equação não tem solução analítica embora seja linear.
,
A solução aproximada, que é pouco precisa para valores altos de , é:
Crie um modelo no SIMULINK para resolver esse problema, e compare a solução com a solução aproximada em .
Passo 1
Neste exercício, vamos solucionar a EDO usando o SIMULINK e vamos comparar a solução com a solução aproximada.
Para resolver uma equação diferencial pelo SIMULINK, a dica é “isolar” a derivada da EDO. Por isso, vamos rearranjar a EDO para:
Desta forma, podemos imaginar: “a derivada é igual a quê?”, localizando onde colocaremos o bloco “Integrator” que nos dará .
Vamos enviar a solução da EDO para um bloco “To Workspace”, para que possamos plotar o resultado junto com a solução aproximada usando o Command Window do MATLAB.
Passo 2
Sabemos que a derivada é igual a , por isso, vamos começar montando o lado direito da equação. Para criar o termo , vamos precisar de dois blocos novos: um bloco “Clock” e um bloco “Trigonometric Function”.
Vá à biblioteca “Sources”, encontre o bloco “Clock” e insira-o em um novo modelo. O bloco “Clock” fornece o tempo de simulação, de forma que podemos usá-lo para construir funções dependentes do tempo. Em outras palavras, ele representará o de .

O bloco “Trigonometric Function” pertence à biblioteca “Math Operations” e ele calcula a função trigonométrica de seu sinal de entrada. Insira um desses blocos no modelo e conecte sua entrada à “Clock”:

Para transformar o “Trigonometric Function” em uma função tangente, clique duas vezes sobre ele para acessar suas propriedades. A propriedade “Function”, destacada abaixo, contém uma lista de funções trigonométricas. Selecione a opção tan e clique em “OK”.
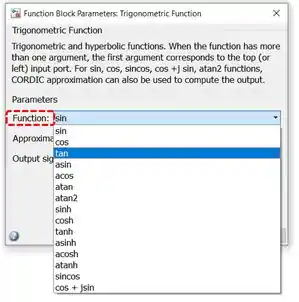
Note que o bloco “Trigonometric Function” mudou de cara:

Passo 3
Para fazer a diferença , insira um bloco “Add” e altere o parâmetro “List of signs” (destacado abaixo), para que uma das entradas de “Add” tenha um sinal negativo, para receber o . Conecte a saída de “Trigonometric Function” à entrada com sinal de “Add”:

Faremos com que a saída de “Add” seja igual a . E é igual a o quê? A ! E é que devemos integrar para encontrar . Por isso, insira um bloco “Integrator”, pertencente à biblioteca “Continuous”, à direita de “Add” e conecte sua entrada à saída de “Add”, como na figura abaixo:

Como a condição inicial da EDO é nula, não precisamos mexer nos parâmetros de “Integrator”, pois o padrão do bloco é ter condição inicial nula.
Passo 4
A saída de “Integrator” será , a solução da nossa EDO. Como queremos gerar o gráfico dela no MATLAB (pois ficará mais fácil de plotar a solução encontrada no SIMULINK com a solução aproximada), vamos inserir um bloco “To Workspace”. Este bloco serve para levar para o “Workspace” do MATLAB os resultados da simulação, permitindo manipulá-los no “Command Window”. Conecte a saída de “Integrator” a entrada de “To Workspace”:
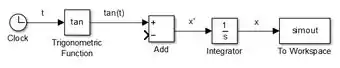
Se você quiser, você pode alterar o nome da variável que receberá o resultado da simulação no “Workspace” do MATLAB, clicando duas vezes sobre o bloco “To Workspace” e mexendo na propriedade “Variable name”. Eu fiz com que minha variável se chamasse .
Agora que temos , podemos fechar nosso diagrama, conectando a entrada com sinal de de “Add” com a seta entre “Integrator” e “To Workspace”:

Passo 5
Troque o tempo de simulação para e rode o programa. Vá ao MATLAB e olhe o “Workspace”. Você verá que apareceram duas variáveis: e , que estão aí graças ao bloco “To Workspace”. é um vetor que contém o tempo de simulação, indo de a . Já contém o resultado da simulação do SIMULINK.
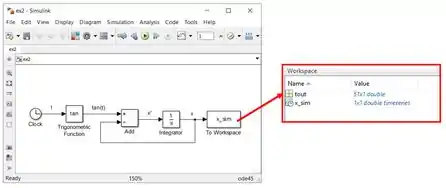
Para gerar o gráfico com a solução da EDO obtida pelo SIMULINK e a solução aproximada, abra um script novo no MATLAB e digite as seguintes linhas de código:
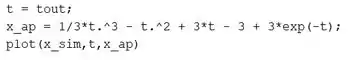
Na primeira linha, criamos um vetor igual ao vetor .
Na segunda linha, calculamos para cada elemento do vetor e armazenamos o resultado no vetor .
Finalmente, na última linha, plotamos as curvas da solução obtida pelo SIMULINK e da solução aproximada. Execute o script e você terá o gráfico.
Quando você executar o programa, o MATLAB vai te pedir para salvar o script. Se for salvá-lo na mesma pasta onde está o arquivo do seu modelo SIMULINK, dê um nome diferente, para não haver conflito.
Resposta

A curva azul é a solução obtida pelo SIMULINK e a curva vermelha, a solução aproximada.
Exercício Resolvido #4
“Adaptado de UnB – 107506: Laboratório de Controle de Processos. Aula: MATLAB. Prof. Eduardo Stockler Tognetti (2018) – Exercício 4”
O nível de um tanque de área de seção transversal , com uma válvula de saída com resistência , é dado por:
Onde representa a vazão de entrada.
Usando o SIMULINK, encontre , sabendo que inicialmente o tanque está com um nível . Considere , e que a vazão de entrada equivale a uma função degrau onde .
Passo 1
Usaremos o SIMULINK para encontrar a solução da equação diferencial do enunciado e plotar seu gráfico. A solução é e corresponde ao nível de um tanque em função do tempo, em horas.
A equação diferencial dada pelo enunciado já está com a derivada isolada no lado esquerdo, facilitando o raciocínio: “a derivada é igual a o quê?”, nos ajudando a identificar onde pôr o boco “Integrator” que nos dará . A saída de “Integrator” será conduzida a um bloco “Scope”, que nos dará o gráfico de .
Passo 2
Vamos atualizar a equação diferencial com as constantes dadas no enunciado:
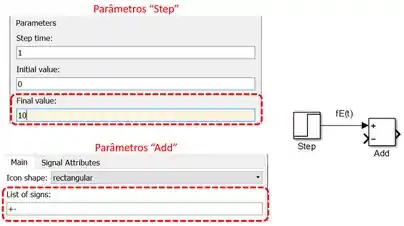
Vemos que a derivada é igual a , por isso, vamos começar modelando o lado direito da equação. Em novo modelo do SIMULINK, insira um bloco “Step” (representando ) e um bloco “Add”. Para o bloco “Step”, mude o parâmetro “Final value” para (destacado), para ele ter o valor da vazão de entrada.
No bloco “Add”, altere o parâmetro “List of signs” (destacado abaixo), para que uma das entradas de “Add” tenha um sinal negativo, para receber o mais pra frente. Conecte a saída de “Step” à entrada com sinal de “Add”:
Passo 3
A saída de “Add” será a diferença . Para que esta diferença seja igual a , ele deve ser multiplicada por . Por isso, vamos colocar um bloco “Gain” à direita de “Add”, fazer com que seu ganho seja igual a e conectar sua entrada à saída de “Add”:
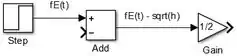
A saída de “Gain” será a derivada , por isso, vamos inserir um bloco “Integrator” à sua direita e conectá-los. Altere o parâmetro “Initial Condition” de “Integrator” para :

Passo 4
A saída de “Integrator” é a solução da equação diferencial . Para gerarmos o seu gráfico, insira um bloco “Scope” e conecte-o a “Integrator”:

Agora que temos , podemos criar o termo da diferença . Para isto, vamos usar um bloco novo, o “Sqrt”, da biblioteca “Math Operations”, que calcula a raiz quadrada de um sinal.

Insira-o no modelo e conecte sua entrada à seta entre o bloco “Integrator” e “Scope”:

Dessa forma, o sinal de vai simultaneamente para “Scope” e para “Sqrt”. “Sqrt” vai nos dar em sua saída , por isso, conecte a saída de “Sqrt” à entrada negativa do bloco “Add”, para obtermos :

O diagrama de blocos representando a equação diferencial está pronto! Para vermos o gráfico de , execute o programa. Como o enunciado não especificou o tempo da simulação, faremos com que seja o padrão de mesmo. Em seguida, clique duas vezes sobre “Scope” para ver o gráfico.
Resposta

Exercício Resolvido #5
“Adaptado de UFG & UCG – EEEC – Introdução ao Programa MATLAB com Aplicações, de Antônio César Baleeiro Alves, Enes Gonçalves Marra e José Wilson Lima Nerys. Exemplo 11.2, p. 63 (2007)”
Considere o sistema massa-mola abaixo:
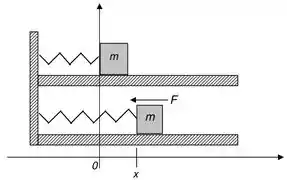
A posição do bloco de massa é representada por , sua velocidade por e sua aceleração por . As equações de movimento da Física nos dizem que e , onde é o tempo.
Pela 2ª lei de Newton, temos que a aceleração do bloco é dada por:
Onde é a rigidez da mola e é igual a .
A energia potencial do sistema é dada por:
E a energia cinética :
Considerando que o bloco parte do repouso, de uma posição inicial , utilize o SIMULINK para:
- Encontrar a solução de , para o intervalo de tempo ;
- Gerar os gráficos da energia potencial e da energia cinética.
Passo 1
Neste exercício, resolveremos uma EDO de segunda ordem, correspondendo à equação que calcula a aceleração pela 2ª lei de Newton. Substituindo e na EDO, temos:
Na letra do exercício, resolveremos a EDO acima, que nos dará , cujo gráfico iremos plotar usando um bloco “Scope”.
A partir do diagrama construído para resolver a letra , faremos a letra , pois o diagrama nos permitirá calcular as energias potencial e cinética do sistema. Ambas as energias também serão plotadas usando um bloco “Scope”.
Passo 2
Vamos começar a solucionar a EDO de segunda ordem. O enunciado no disse que e , logo:
Com essas informações podemos construir um diagrama inicial, inserindo em um novo modelo dois blocos “Integrator” e um bloco “Scope”, da seguinte forma:
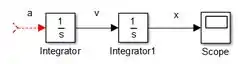
O primeiro “Integrator” receberá um sinal representando a aceleração , fará sua integração e nos dará a velocidade . entrará em um segundo bloco “Integrator” para obtermos , que é conduzido a um bloco “Scope” para plotarmos seu gráfico mais pra frente.
O enunciado diz que o bloco parte do repouso, indicando que a velocidade inicial é . Por isso, não precisamos alterar o parâmetro “Initial condition” do “Integrator” que recebe , pois o padrão do bloco “Integrator” é ter condição inicial nula.
Contudo, este não é o caso do segundo “Integrator”, que recebe o sinal de velocidade . O enunciado diz que o bloco parte da posição , por isso, temos que alterar o parâmetro “Initial condition” do “Integrator” que integra a velocidade e nos dá a posição (destacado abaixo):
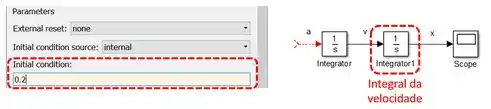
Passo 3
Com esse diagrama inicial, podemos partir para a EDO de segunda ordem para obtermos a aceleração . Insira no modelo um bloco “Gain” e altere seu ganho para :
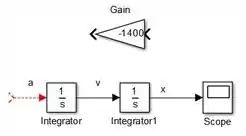
Queremos criar o termo , por isso, conecte a entrada de “Gain” à seta entre “Integrator1” e “Scope”:
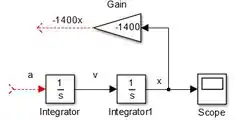
A saída de “Gain” será . E quam é igual a ? A aceleração ! Por isso, conecte a saída de “Gain” à entrada do primeiro “Integrator”, que ainda está vazia:
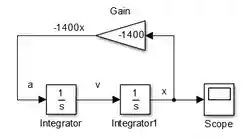
O diagrama que nos dá a solução da letra a do exercício está pronto! Com ele, podemos obter o gráfico de , que é a solução de . Para isto, altere o tempo de simulação de para , rode o programa e clique duas vezes sobre o “Scope” para ver o gráfico:
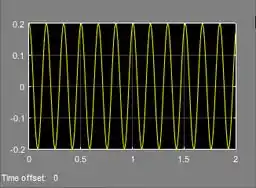
Pronto, letra a resolvida =)
Passo 4
A letra b do exercício pede para gerarmos os gráficos das energias potencial e cinética. A energia potencial é dada por , com . Logo, . Para obtermos a partir do diagrama construído para resolver a letra , vamos começar obtendo Para isto, usaremos o bloco “Product”, da biblioteca “Math Operations”, e faremos com que o sinal de entre em suas duas entradas:

Para calcular , insira um bloco “Gain”, faça-o ter um ganho igual a e conecte sua entrada à saída de “Product”:

A saída do bloco “Gain1” será a energia potencial .
Passo 5
A energia cinética é dada por , com . Logo, . Para obtermos a partir do diagrama construído para resolver a letra , vamos começar obtendo Para isto, usaremos outro bloco “Product”, que receberá o sinal de em suas duas entradas:
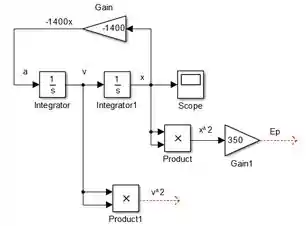
Para calcular , insira outro bloco “Gain”, faça-o ter um ganho igual a e conecte sua entrada à saída de “Product1”:

A saída do bloco “Gain2” será a energia cinética .
Vamos plotar as curvas de e no mesmo gráfico, conectando as duas saídas que dão de e a cada uma das entradas de um bloco “Mux”. A saída de “Mux” se conectará a um bloco “Scope”:
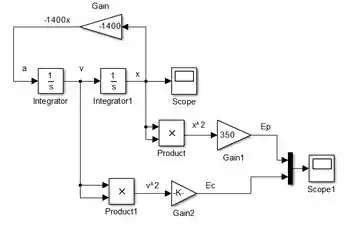
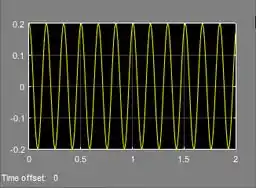
Como está conectado à entrada de cima de “Mux”, sua curva será amarela. Já a curva de será rosa, pois entra na entrada na de baixo de “Mux”.
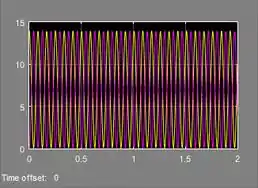
Execute o programa e você terá o gráfico de ambas as energias.
Resposta
- A solução de é:
- A curva da energia potencial é a onda amarela e a curva da energia cinética é rosa.
Exercício Resolvido #6
“UFMG – Learning.m: Uma apostila de introdução às ferramentas do MATLAB. PET Engenharia Elétrica (2020). Exercício 10.9”
Modele a seguinte equação diferencial e observe o gráfico:
Passo 1
Neste exercício, vamos resolver uma EDO de segunda ordem pelo SIMULINK. Comece pela dica de isolar a derivada de maior ordem da EDO:
Desta forma, fica mais fácil identificar onde colocaremos o bloco “Integrator” (nesse caso, utilizaremos dois, pois a EDO tem uma segunda derivada) e qual bloco da biblioteca “Sources” utlizaremos para começar a construir o modelo.
O primeiro bloco “Integrator” nos dará e o segundo, , que é a solução da EDO.
Ao final, geraremos o gráfico de usando um bloco “Scope”.
Passo 2
Vamos começar modelando o lado direito da EDO: . O pode ser modelado por um bloco “Constant”, da biblioteca “Sources”, e as operações de subtração serão feitas por meio de um bloco “Add”.
Faça com que o bloco “Constant” seja igual a . Por padrão, o bloco “Add” possui duas entradas positivas. Altere seus parâmetros para que ele passe a ter uma entrada positiva e duas negativas, trocando o por no parâmetro “List of signs”:

Conecte “Constant” à entrada positiva de “Add”. As entradas negativas de “Add” receberão e mais para frente, por isso, a saída de “Add” será .
Passo 3
Para obter , insira um bloco “Integrator” e conecte a saída de “Add” à entrada deste bloco. Desta forma, estaremos integrando para gerar .
![]()
Como , não precisamos alterar o parâmetro “Initial condition” de “Integrator”, pois as condições iniciais são nulas por padrão.
Agora que temos , vamos inserir mais um bloco “Integrator” para obter . Coloque-o à direita do primeiro “Integrator” inserido e conecte-os:

Novamente, não precisamos mudar os parâmetros do segundo “Integrator” inserido, pois e por padrão as condições iniciais de “Integrator” são nulas.
Insira um bloco “Scope” e conecte sua entrada à saída de “Integrator1”, para que tenhamos o gráfico de .

Passo 4
Vamos terminar de modelar o lado direito da EDO: , começando por . Insira um bloco “Gain” no modelo e altere seu ganho para . Em seguida, conecte sua entrada à flecha entre os dois blocos “Integrator” (pois é ali que temos o sinal representando ) . Conecte a saída de “Gain” a uma das entradas negativas de “Add”:

Para modelar , o procedimento é igualzinho. Insira outro bloco “Gain” e mude o ganho para . Então, conecte a entrada desse “Gain” igual a à flecha conectando o bloco “Integrator1” a “Scope”, pois é onde temos o sinal de . Para finalizar o modelo, conecte a saída de “Gain1” à última entrada negativa de “Add”:

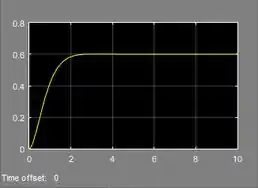
Voilà! EDO modelada! Para ver o gráfico de , basta rodar a simulação.
Resposta
Exercício Resolvido #7
“Adaptado de MATLAB for Engineering Applications, de William J. Palm III. Seção 11.4, exercício 35, p. 504”
A seguinte equação descreve ao temperatura de um certo objeto imerso em um líquido com temperatura constante .
Suponha que a temperatura inicial do objeto é e a temperatura do líquido é. Utilizando o SIMULINK:
- Plote a temperatura do objeto em função do tempo;
- Em quanto tempo a temperatura do objeto atingirá a temperatura do líquido?
Passo 1
Neste exercício, resolveremos a EDO para encontrar usando o SIMULINK. Geraremos o gráfico de para resolver a letra a e usaremos o gráfico para responder a letra b.
Para resolver uma EDO no SIMULINK, a dica é isolar a derivada de maior ordem da EDO, logo:
Desta forma, conseguimos identificar onde colocaremos o bloco “Integrator” e qual bloco da biblioteca “Sources” podemos usar para começar a modelar a EDO.
Passo 2
Vamos começar modelando a diferença . Em um novo modelo do SIMULINK, insira um bloco “Constant” e faça com que seu valor seja igual a . Em seguida, insira um bloco “Add” e altere seus parâmetros, de forma que ele tenha um entrada positiva e outra negativa:
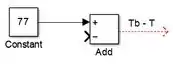
O bloco “Add” receberá o sinal de mais para frente, por isso, a saída de “Add” será .
Para termos , insira um bloco “Gain”, faça com que seu ganho seja igual a e conecte sua entrada à saída de “Add”:

A saída de “Gain” será . E quem é igual ? É ! Por isso, a saída de “Gain” será igual à derivada da nossa EDO.
Passo 3
Isso significa que temos que adicionar um bloco “Integrator” à direita de “Gain” e conectar a saída de “Gain” à entrada de “Integrator”. Desta forma, “Integrator” nos dará . Não esqueça de mudar o parâmetro “Initial condition” de “Integrator” de para , pois .

Para termos o gráfico de , insira um bloco “Scope” e conecte-o a “Integrator”:

Passo 4
Para finalizar o modelo, leve o sinal de até a entrada negativa de “Add”:
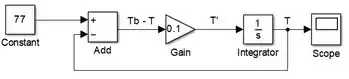
A EDO está modelada! Vamos ver o gráfico de , executando a simulação e clicando duas vezes sobre “Scope”:
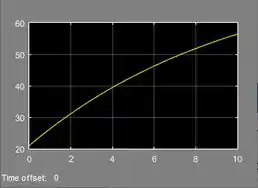
Rodei a simulação para . Contudo, note que o eixo vertical do gráfico vai só até e na letra queremos saber quanto tempo o objeto demora para atingir a temperatura do líquido, isto é, . Temos que aumentar o tempo de simulação para que a curva do gráfico atinja essa temperatura. Aumente o tempo para :
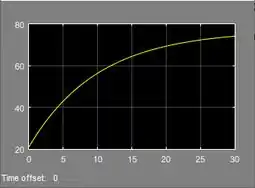
Agora o eixo vertical vai até , pode ser que agora encontremos a temperatura de .
Passo 5
Para vermos os valores da curva, na janela do “Scope”, clique em “Try Time Scope” e o use o “Cursor Measurements”:

Leve o cursor até o início da curva, onde teremos (destacado em amarelo abaixo). Arraste o cursor até o final da curva para vermos a temperatura do objeto em (destacado em vermelho abaixo).

Note que e queremos saber o tempo que demora para que o objeto tenha um temperatura igual a . Por isso, devemos aumentar o tempo de simulação até que consigamos que o cursor nos retorne um valor igual ou muito próximo de .
Passo 6
Sem fechar a janela do “Scope” com o gráfico e os cursores, aumente o tempo de simulação e rode o programa novamente. O gráfico se atualizará automaticamente. Faça esse procedimento até que o cursor retorne .
Eu fui aumentando o tempo de simulação até , quando finalmente encontrei o valor (destacado em vermelho abaixo):
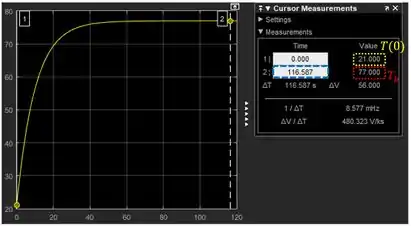
O tempo que o objeto demora para que sua temperatura atinja é dado pelo campo destacado em azul acima: .
Resposta
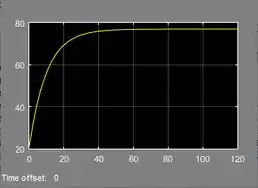
- Gráfico de :
- A temperatura do objeto atinge em .
Exercício Resolvido #8
“Adaptado de Sistemas Dinâmicos I: Usando a ferramenta MATLAB, da USP, elaborado por Eduardo L. L. Cabral e Larissa Driemeier. Exercício 13.4.2, p. 87”
Essa atividade consiste em resolver a equação diferencial que representa a dinâmica de um sistema massa-mola-amortecedor não linear. Um sistema massa mola-amortecedor não linear é representado pelas seguinte equação diferencial:
Onde é a posição da massa e é a força aplicada na massa.
Simule o sistema para a condição inicial e e para a força variando na forma de um degrau de amplitude igual a , no intervalo de tempo entre e segundos. Apresente os gráficos da posição, velocidade e força.
Passo 1
Neste exercício, resolveremos uma equação diferencial de 2ª ordem não-linear usando o SIMULINK. Apesar de a equação ser não-linear, a dica de isolar a derivada de maior ordem ainda está valendo:
Desta forma, identificamos onde colocaremos os dois blocos “Integrator” que precisamos para encontrar (usaremos um bloco “Integrator” para integrar e obter ; e outro “Integrator” que receberá o , o integrará e nos dará ) e por onde começamos a construir o diagrama de blocos.
O enunciado pede para plotarmos os gráficos da posição, da velocidade e da força, ou seja, os gráficos de , e , respectivamente. Para gerarmos os gráficos pedidos pelo enunciado, usaremos três blocos “Scope”, uma para cada gráfico.
Passo 2
Vamos começar o diagrama pelo lado direito da equação: , mais especificamente por . é um degrau de amplitude , por isso, em um modelo novo, insira um bloco “Step” e altere sua propriedade “Final value” para .
Em seguida, insira um bloco “Add” e troque sua propriedade “List of signs” de por , para que “Add” tenha três entradas, uma com sinal as outras duas com sinal . Conecte o “Step” à entrada positiva de “Add”:

As outras duas entradas de “Add” receberão e , portanto, a saída de “Add” será igual a , que é igual a . Logo, a saída de “Add” será e é nele que devemos conectar um bloco “Integrator”.
Passo 3
Insira um bloco “Integrator” no modelo e conecte sua entrada à saída de “Add”:
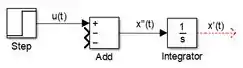
Este bloco “Integrator” integrará e nos dará . Como , não precisamos alterar a propriedade “Initial condition” de “Integrator”, pois por padrão ela já é igual a .
Para obter , insira outro bloco “Integrator” e conecte sua entrada à saída do primeiro bloco “Integrator”. Em outras palavras, o segundo bloco “Integrator” receberá , o integrará e fornecerá . Como , mude a propriedade “Initial condition” do “Integrator” que calculará (destacado abaixo) para esse valor:
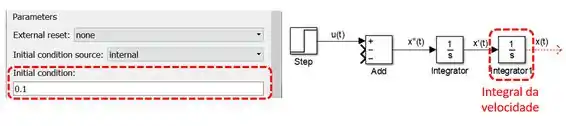
Para gerar o gráfico de , insira um bloco “Scope” e conecte-o ao “Integrator” que calcula a posição :
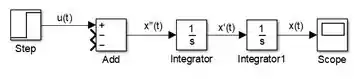
Passo 4
Precisamos terminar de modelar o lado direito da equação: . Vamos começar por . Para calcular , insira um bloco “Product” e faça com que suas duas entradas recebam , conectando cada entrada à flecha entre os dois blocos “Integrator” (que corresponde ao sinal de ):
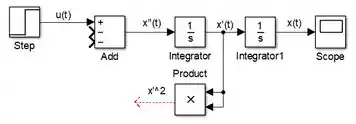
Em seguida, insira um bloco “Gain”, faça com que seu ganho seja igual a e conecte sua entrada à saída de “Product”. Conecte a saída de “Gain” com uma das entradas negativas de “Add”. Dessa forma, já temos :
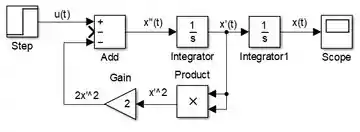
Passo 5
Vamos modelar o termo . Para calcular , usaremos o bloco “Math Function”, da biblioteca “Math Operations”:
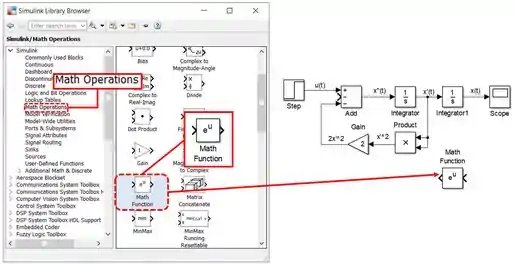
Este bloco aplica uma função matemática em sua entrada e retorna o resultado. Ele inclui funções como exponenciação, módulo e, o que interessa pra gente, logaritmo. Para calcular , conecte a entrada do bloco “Math Function” à flecha entre “Integrator1” e “Scope” (que representa o sinal de ) e altere a propriedade “Function” do bloco “Math Function” para :
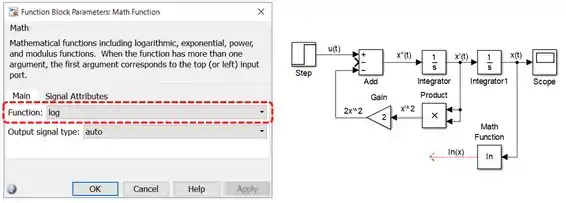
No SIMULINK, assim como no MATLAB, o logaritmo natural, isto é, o , é representado por . Quando queremos calcular o logaritmo na base de algum número, usamos (repare que tem essa opção também no prâmetro “Function”).
Quando você fizer a alteração, note que o bloco “Math Funtion” muda de cara, passando a ter um dentro dele.
Para terminar o termo , insira outro bloco “Gain” e faça com que seu ganho seja igual a . Em seguida, conecte a entrada de “Gain” com ganho à saída de “Math Function” e sua saída, à entrada negativa restante de “Add”:
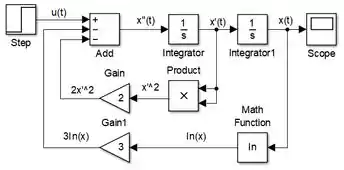
Pronto! A equação diferencial está modelada!
Passo 6
No diagrama atual, conseguimos apenas gerar o gráfico de . Para plotar e , insira mais dois blocos “Scope” e conecte um ao sinal de e outro ao sinal de :
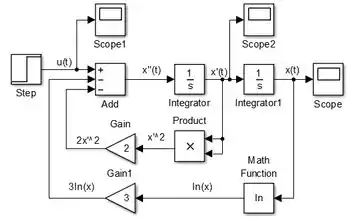
O enunciado pediu para simularmos o sistema de a , que já é o tempo de simulação padrão do SIMULINK. Por isso, não precisamos alterá-lo e já podemos executar o programa para vermos os gráficos de , e .
Resposta
Gráfico da posição
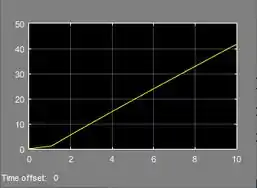
Gráfico da velocidade
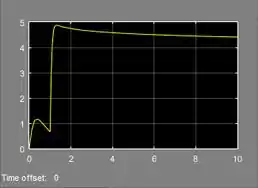
Gráfico da força